题目内容
6.一只不透明的袋子中装有1个白球、1个蓝球和2个红球,这些球除颜色外都相同.(1)从袋中随机摸出1个球,摸出红球的概率为$\frac{1}{2}$;
(2)从袋中随机摸出1个球(不放回)后,再从袋中余下的3个球中随机摸出1个球.求两次摸到的球颜色不相同的概率.
分析 (1)直接利用概率公式求出摸出红球的概率;
(2)利用树状图得出所有符合题意的情况,进而理概率公式求出即可.
解答 解:(1)从袋中随机摸出1个球,摸出红球的概率为:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)如图所示: ,
,
所有的可能有12种,符合题意的有10种,故两次摸到的球颜色不相同的概率为:$\frac{10}{12}$=$\frac{5}{6}$.
点评 此题主要考查了树状图法求概率,根据题意利用树状图得出所有情况是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
16.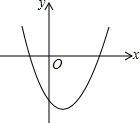 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )| A. | 函数图象与y轴的交点坐标是(0,-3) | |
| B. | 顶点坐标是(1,-3) | |
| C. | 函数图象与x轴的交点坐标是(3,0)、(-1,0) | |
| D. | 当x<0时,y随x的增大而减小 |
11.要使二次根式$\sqrt{3-2x}$有意义,则x的取值范围是( )
| A. | x$≥\frac{3}{2}$ | B. | x$≤\frac{3}{2}$ | C. | x$≥\frac{2}{3}$ | D. | x$≤\frac{2}{3}$ |
15.某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是甲组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
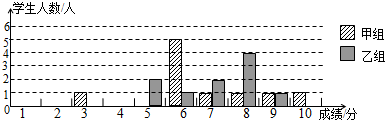
(1)补充完成下列的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲 | 6.7 | 6 | 3.41 | 90% | 20% |
| 乙 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.

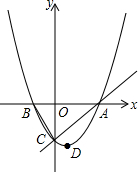 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
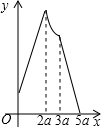
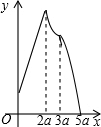
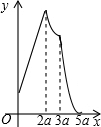
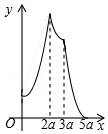
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.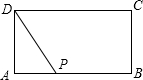 如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )