��Ŀ����
2��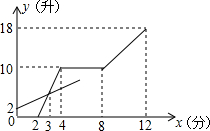 ���мס��������������ֱ�װ�н�ˮ�ܺͳ�ˮ�ܣ��������Ľ���ˮ�ٶȲ��䣬�ȴ��������Ľ�ˮ�ܣ�2����ʱ�ٴ������Ľ�ˮ�ܣ��ֹ�2���ӹرռ������Ľ�ˮ�ܣ��ٹ�4����ͬʱ�������Ľ�����ˮ�ܣ�ֱ��12����ʱ��ͬʱ�ر��������Ľ���ˮ�ܣ��ر�ˮ�ܵ�ʱ����Բ��ƣ������е�ˮ��y��������������עˮʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ��
���мס��������������ֱ�װ�н�ˮ�ܺͳ�ˮ�ܣ��������Ľ���ˮ�ٶȲ��䣬�ȴ��������Ľ�ˮ�ܣ�2����ʱ�ٴ������Ľ�ˮ�ܣ��ֹ�2���ӹرռ������Ľ�ˮ�ܣ��ٹ�4����ͬʱ�������Ľ�����ˮ�ܣ�ֱ��12����ʱ��ͬʱ�ر��������Ľ���ˮ�ܣ��ر�ˮ�ܵ�ʱ����Բ��ƣ������е�ˮ��y��������������עˮʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ����1����������Ľ�����ˮ�ٶȣ�
��2��������������ˮ�ܶ��رպ��Ƿ������������ˮ����ȣ������ڣ������ʱ��ʱ�䣮
��3����ʹ��������12����ʱˮ����ȣ���������6���Ӻ��ˮ�ٶ�Ӧ��Ϊ���٣�
���� ��1������ͼʾ֪������������2�����ڽ�ˮ��Ϊ10����
��2����ͼ��֪���������ڵ�3����ʱˮ��Ϊ��5����3-2��=5����������A��3��5������y��=kx+b��k��0�������ô���ϵ������øú�������ʽ����y=10������ֵ���ɣ�
��3��ʹ��������12����ʱˮ�����ʱ����x=6ʱ��y��=8���ʣ�18-8���£�12-6��=$\frac{5}{3}$����/�֣���
��� �⣺��1���Ľ�ˮ�ٶȣ�$\frac{10}{4-2}$=5����/�֣���
�ij�ˮ�ٶȣ�5-$\frac{18-10}{12-8}$=3����/�֣���
��2�����ڣ�
��ͼ��֪���������ڵ�3����ʱˮ��Ϊ��5����3-2��=5����������A��3��5����
��y��=kx+b��k��0����������ã�
$\left\{\begin{array}{l}{3k+b=5}\\{b=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$��
����y��=x+2��
��y��=10ʱ��x=8��
������������ˮ�ܴ�8����ʱ��������ˮ����ȣ�
��3����x=6ʱ��y��=8��
���ԣ�18-8���£�12-6��=$\frac{5}{3}$����/�֣���
����������6���Ӻ��ˮ���ٶ�Ӧ��Ϊ$\frac{5}{3}$��/�֣�
���� ���⿼����һ�κ�����Ӧ�ã���һ�κ������⣺�ٽ�������ģ�͵ķ������ڷֶκ���˼���Ӧ�ã�

 ��У����ϵ�д�
��У����ϵ�д�| A�� | -2 | B�� | 2 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
| A�� | x$��\frac{3}{2}$ | B�� | x$��\frac{3}{2}$ | C�� | x$��\frac{2}{3}$ | D�� | x$��\frac{2}{3}$ |
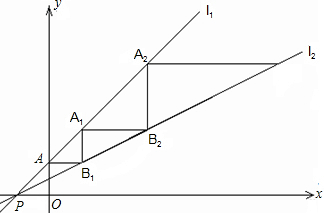 ��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=$\frac{1}{2}$x+$\frac{1}{2}$�ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶����ﵽֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������B2015��A2015��������C����A2015��ʱ���˶�����·���ij�Ϊ��������
��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=$\frac{1}{2}$x+$\frac{1}{2}$�ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶����ﵽֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������B2015��A2015��������C����A2015��ʱ���˶�����·���ij�Ϊ��������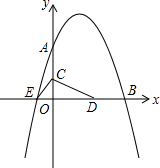 ��ͼ����֪������y=-$\frac{1}{2}$x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
��ͼ����֪������y=-$\frac{1}{2}$x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���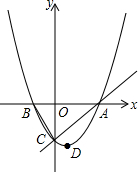 ��ͼ����֪������y=ax2+bx+c�Ķ���D������Ϊ��1��-$\frac{9}{2}$��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm��
��ͼ����֪������y=ax2+bx+c�Ķ���D������Ϊ��1��-$\frac{9}{2}$��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm�� ��ͼ��ʾ�ļ������������С��������϶��ɵģ���������ͼ�ǣ�������
��ͼ��ʾ�ļ������������С��������϶��ɵģ���������ͼ�ǣ�������



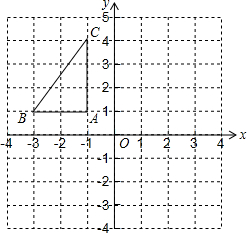 ��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�Ϊ
��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�Ϊ