题目内容
1．已知平面直角坐标系中的点P（a-1，a+2）在第二象限，则a的取值范围是-2＜a＜1．分析 根据平面直角坐标系中第二象限内的点的横坐标小于0，纵坐标大于0，可得$\left\{\begin{array}{l}{a-1＜0}\\{a+2＞0}\end{array}\right.$；然后根据解一元一次不等式组的方法，求出a的取值范围即可．
解答 解：∵平面直角坐标系中的点P（a-1，a+2）在第二象限，
∴$\left\{\begin{array}{l}{a-1＜0}\\{a+2＞0}\end{array}\right.$
解得-2＜a＜1，
即a的取值范围是：-2＜a＜1．
故答案为：-2＜a＜1．
点评 （1）此题主要考查了点的坐标问题，要熟练掌握，解答此题的关键是要明确各个象限内点的横坐标和纵坐标的正负情况．
（2）此题还考查了解一元一次不等式组问题，要熟练掌握，解答此题的关键是要明确解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
相关题目
如图，点A在数轴上对应的数为2，若点B也在数轴上，且线段AB的长为4，C为OB的中点，则点C在数轴上对应的数为-1或3．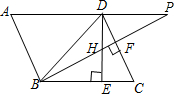
如图，在平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线交于P．下面结论：
6．
如图，在△ABC中，∠ACB=90°，CD是AB边上的高，如果∠A=50°，则∠DCB=（ ）
如图，在△ABC中，∠ACB=90°，CD是AB边上的高，如果∠A=50°，则∠DCB=（ ）| A． | 50° | B． | 45° | C． | 40° | D． | 25° |