题目内容
10.特值验证:当x=-1,0,1,2,5,…时,计算代数式x2-2x+2的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式x2-2x+2的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:
我们可以用学过的知识,对x2-2x+2进行恒等变形:x2-2x+2=(x2-2x+1)+1=(x-1)2+1. (注:这种变形方法可称为“配方”)∵(x-1)2≥0,∴(x-1)2+1≥1.
所以无论x取何值,代数式x2-2x+2的值不小于1,即最小值为1.
迁移实证:
(1)请你用“配方”的方法,确定2x2-8x+11的最小值为3;
(2)求-x2+6x-10的最大值.
分析 (1)根据配方法可以说明2x2-8x+11的最小值为3;
(2)根据配方法可以求得-x2+6x-10的最大值.
解答 解:(1)2x2-8x+11
=2(x2-4x)+11
=2(x-2)2+3,
∴当x=2时,2x2-8x+11取的最小值,最小值是3;
(2)-x2+6x-10
=-(x2-6x)-10
=-(x-3)2-1,
∴当x=3时,-x2+6x-10取得最大值,最大值是-1,
即-x2+6x-10的最大值是-1.
点评 本题考查配方法的应用,解答本题的关键是明确题意,利用配方法解答问题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
18.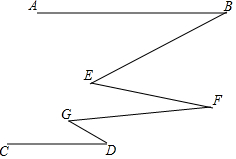 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )| A. | ∠D=∠F=∠B | B. | ∠B+∠F+∠D=60° | C. | ∠B+∠F+∠D=120° | D. | GD∥EF |
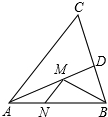 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$. 如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.
如图:⊙O的直径AB⊥CD于P,AP=CD=4cm,则OP=$\frac{5}{2}$cm.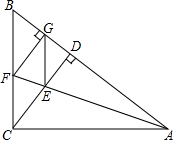 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.