Question

20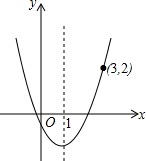．已知函数y=ax²+bx-1的图象经过点（3，2），对称轴为直线x=1．
（1）求这个函数的解析式；
（2）当x＞0时，求使y≥2的x的取值范围．

Answer 1

分析 （1）根据对称轴为直线x=可得-$\frac{b}{2a}$=1，将点（3，2）代入可得关于a、b的方程，联立方程组求得a、b的值即可；
（2）由y≥2可得关于x的不等式，解不等式结合x＞0可得x的取值范围．

解答 解：（1）根据题意，知：$\left\{\begin{array}{l}{9a+3b-1=2}\\{-\frac{b}{2a}=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$，
故该函数解析式为：y=x²-2x-1；

（2）当y≥2时，有x²-2x-1≥2，
解得：x≤-1或x≥3，
又∵x＞0，
∴x≥3．

点评 主要考查了待定系数法求二次函数的解析式和函数图象的性质，要会根据图象所在的位置关系求相关的变量的取值范围．