题目内容
12.解不等式:x2-2x≥3.分析 先把不等式整理成x2-2x-3≥0,然后写出抛物线y=x2-2x-3不在x轴下方部分的x的取值范围即可.
解答 解:不等式可化为x2-2x-3≥0,
抛物线y=x2-2x-3≥0与x轴相交时y=0,
所以x2-2x-3=0,
解得x1=-1,x2=3.
故不等式的解集是x≤-1或x≥3.
点评 本题考查了二次函数与不等式,此类题目关键在于求出抛物线与x轴的交点的x的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列计算正确的是( )
| A. | 3x2•2x=6x3 | B. | x6÷x3=x2 | C. | (3a)2=3a2 | D. | (a+b)2=a2+b2 |
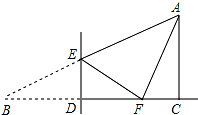 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.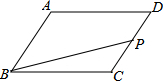 如图所示是边长为2的菱形ABCD,∠ABC=60°,点P在CD上,且从点C运动到点D,线段CP=x,四边形ABPD的面积为y.
如图所示是边长为2的菱形ABCD,∠ABC=60°,点P在CD上,且从点C运动到点D,线段CP=x,四边形ABPD的面积为y.