题目内容
2.函数y=x2+bx+c的顶点在x轴且顶点横坐标为2,则b=-4,c=4.分析 根据抛物线顶点横坐标为2,可知:$-\frac{b}{2a}=2$,从而可求得b的值,然后根据顶点在x轴上可知,b2-4ac=0,从而可求得c的值.
解答 解:∵抛物线的顶点横坐标为2,
∴$-\frac{b}{2}=2$.
∴b=-4.
∵抛物线顶点在x轴上,
∴b2-4ac=0,即(-4)2-4×1×c=0.
解得:c=4.
故答案为:-4;4.
点评 本题主要考查的是二次函数的性质,根据抛物线顶点在x轴且顶点横坐标为2,得出关于b、c方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.八边形的内角和等于( )
| A. | 360° | B. | 1080° | C. | 1440° | D. | 2160° |
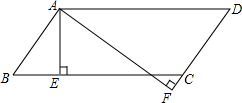 如图,在?ABCD中,AE⊥BC于E,AF⊥DC于DC延长线上一点F,AE=3cm,AF=5cm,∠EAF=30°,求?ABCD各角度数、周长及面积.
如图,在?ABCD中,AE⊥BC于E,AF⊥DC于DC延长线上一点F,AE=3cm,AF=5cm,∠EAF=30°,求?ABCD各角度数、周长及面积.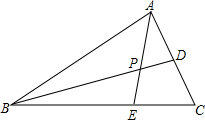 如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.
如图,在△ABC中,点D、E分别在AC、BC边上,且AD=CD,BE=2CE,AE与BD交于P点.若△ABC的面积为1,求四边形CDPE的面积.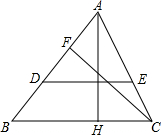 如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.
如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.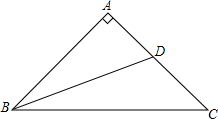 如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.
如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.