题目内容
20.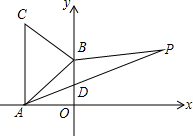 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.(1)求△ABC的面积;
(2)用含a的代数式表示△ABP的面积;
(3)若2S△ABP=S△ABC,求点D的坐标.
分析 (1)根据A(-$\sqrt{3}$,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,
(2)过P点作PD⊥x轴,垂足为D,利用S△ABP=S△AOB+S梯形BODP-S△ADP即可表示出△ABP的面积;
(3)根据2S△ABP=S△ABC列方程求得a,根据待定系数法求得直线PA的解析式,即可求得D的坐标.
解答 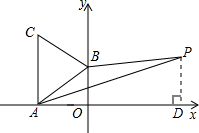 解:(1)由A(-$\sqrt{3}$,0)、B(0,1)得OA=$\sqrt{3}$,OB=1,
解:(1)由A(-$\sqrt{3}$,0)、B(0,1)得OA=$\sqrt{3}$,OB=1,
∴tan∠OAB=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=90°,
由勾股定理,得AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2,
∴S△ABC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$;
(2)过P点作PD⊥x轴,垂足为D,
S△ABP=S△AOB+S梯形BODP-S△ADP
=$\frac{1}{2}$×$\sqrt{3}$×1+$\frac{1}{2}$×(1+a)×3-$\frac{1}{2}$×($\sqrt{3}$+3)×a,
=$\frac{\sqrt{3}+3-\sqrt{3}a}{2}$,
(3)由2S△ABP=S△ABC,$\sqrt{3}+3-\sqrt{3}$a=$\sqrt{3}$,
∴a=$\sqrt{3}$.
∴P(3,$\sqrt{3}$),
设直线AP的解析式为y=kx+b,
代入P(3,$\sqrt{3}$),A(-$\sqrt{3}$,0)得$\left\{\begin{array}{l}{3k+b=\sqrt{3}}\\{-\sqrt{3}k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}-1}{2}}\\{b=\frac{3-\sqrt{3}}{2}}\end{array}\right.$
∴D(0,$\frac{3-\sqrt{3}}{2}$).
点评 本题考查了等边三角形的性质,坐标和图形的性质,不规则三角形面积的表示方法及待定系数法求解析式.

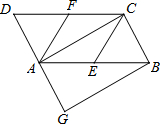 如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.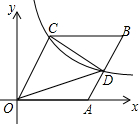 如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$).
如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$). 如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( )
如图,△ABC为等边三角形,∠ABC的平分线与∠ACB的平分线交于点O,过点O作平行于BC的直线,交AB于M,交AC于N,连接AO,则图中等腰三角形(不含等边三角形)的个数有( ) 已知A、B、C、D四点如图所示,请按如图的要求作图
已知A、B、C、D四点如图所示,请按如图的要求作图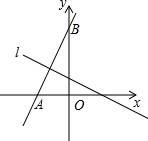 如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$.
如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$. 如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.
如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.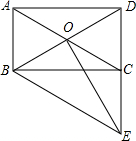 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,连接OE.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,连接OE.