题目内容
20.己知二次数y=x2-4x+3的图象与x轴分别交于点A、B(A在B的左侧),与y轴交于点C,在图象的对称轴上存在一点P使得PA+PC有最小值,通过计算得出其最小值为3$\sqrt{2}$.分析 在图象的对称轴上存在一点P使得PA+PC有最小值,根据A、B关于对称轴对称,PA+PC=PB+PC最小,根据两点之间线段最短可知线段BC即为所求.
解答 解:∵二次数y=x2-4x+3的图象与x轴分别交于点A、B(A在B的左侧),
当y=0时,0=x2-4x+3,
解得:x1=1,x2=3,
∴A(1,0)、B(3,0),对称轴为x=2,
当x=0时,y=3,
∴C(0,3),
当点P是其对称轴上一动点,PA+PC取得最小值时,根据两点之间线段最短,线段BC即为所求,
根据勾股定理BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题主要考查了点的坐标和待定系数法以及线段和最小值问题,建立模型解决最小值问题是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
15. 如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )
如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )
 如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )
如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )| A. | 6cm | B. | 3cm | C. | 5$\sqrt{3}$cm | D. | 3$\sqrt{5}$cm |
12.如果(anbm)3=a9b12,那么m,n的值为( )
| A. | m=9,n=-4 | B. | m=3,n=4 | C. | m=4,n=3 | D. | m=9,n=6 |
10.设m+n=mn,则$\frac{1}{m}+\frac{1}{n}$的值是( )
| A. | $\frac{1}{mn}$ | B. | 0 | C. | 1 | D. | -1 |
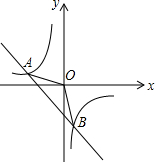 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1),B(1,n)两点. 在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F,则∠DFE=75°.
在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F,则∠DFE=75°.