题目内容
8.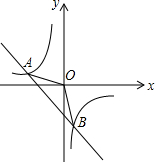 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1),B(1,n)两点.(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
分析 (1)把A(-2,1)代入求出反比例函数的解析式,代入求出A的坐标,把A、B的坐标代入得到方程组,求出方程组的解即可;
(2)求出直线AB与x轴的交点C的坐标,根据三角形的面积公式求出即可.
解答 解:(1)把A(-2,1)代入反比例函数y=$\frac{m}{x}$得:m=-2×1=-2,
∴反比例函数为y=-$\frac{2}{x}$,
把B(1,n)代入得:n=-2,
∴B(1,-2),
把A(-2,1),B(1,-2)代入得:$\left\{\begin{array}{l}{-2k+b=}\\{k+b=-2}\end{array}\right.$,
解得:k=-1,b=-1,
∴一次函数的解析式为y=-x-1.
(2)设直线AB和x轴的交点为C,
令y=0,则0=-x-1,
∴x=-1,
∴C(-1,0),
∴OC=1,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=1.5.
点评 本题主要考查对一次函数与反比例函数的交点问题,用待定系数法求一次函数和反比例函数的解析式,三角形的面积,解一元一次方程,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
18.化简(1+$\frac{1}{a-1}$)÷$\frac{a}{{a}^{2}-2a+1}$的结果是( )
| A. | $\frac{a}{(a-1)^{2}}$ | B. | a-1 | C. | $\frac{1}{a}$ | D. | $\frac{a-1}{a}$ |
19.如图,把图①中的⊙A经过平移得到⊙O(如图②),如果图①中⊙A上一点P的坐标为(m,n),那么平移后在图②中的对应点P′的坐标为( )
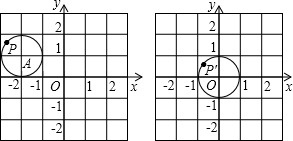

| A. | (m+2,n+1) | B. | (m-2,n-1) | C. | (m-2,n+1) | D. | (m+2,n-1) |
13.下列命题中.不正确的是( )
| A. | 直径是经过圆心的弦 | |
| B. | 半径相等的两个半圆是等弧 | |
| C. | 三角形的内心到三角形各顶点的距离相等 | |
| D. | 经过不共线三点必作一个圆 |

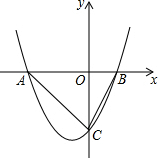 抛物线y=x2+x-2交x轴于点A、B,交y轴于点C,
抛物线y=x2+x-2交x轴于点A、B,交y轴于点C,