题目内容
9. 在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F,则∠DFE=75°.
在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F,则∠DFE=75°.
分析 把△BCE逆时针旋转90°得到△ABG,连接DG、AC、AG.则∠GBE=90°,∠BAG=∠BCE;先证明G、A、C在一条直线上,得出∠DAG=∠BAG,由SAS证明△AGB≌△AGD,得出BG=DG=BE=BD,△BGD为等边三角形,得出∠GBD=60°,求出∠DBE,再由三角形的外角性质即可得出结果.
解答 解:如图所示, 把△BCE逆时针旋转90°得到△ABG,连接DG、AC、AG.
把△BCE逆时针旋转90°得到△ABG,连接DG、AC、AG.
则∠GBE=90°,∠BAG=∠BCE,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=AD,∠BAC=∠DAC=∠BDC=45°,
∴∠BCE=90°+45°=135°,
∵∠BAG=∠BCE=135°,
∴∠BAG+∠BAC=180°,
∴G、A、C在一条直线上,
∴∠DAG=180°-45°=135°=∠BAG,
在△AGB与△AGD中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAG=∠DAG}&{\;}\\{AG=AG}&{\;}\end{array}\right.$,
∴△AGB≌△AGD(SAS),
∴BG=DG=BE=BD,
∴△BGD为等边三角形,
∴∠GBD=60°,
∴∠DBE=90°-60°=30°,
∴∠DFE=∠DBE+∠BDC=30°+45°=75°;
故答案为:75°.
点评 本题考查了正方形的性质、旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、三点共线;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
19.如图,把图①中的⊙A经过平移得到⊙O(如图②),如果图①中⊙A上一点P的坐标为(m,n),那么平移后在图②中的对应点P′的坐标为( )
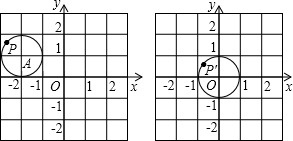

| A. | (m+2,n+1) | B. | (m-2,n-1) | C. | (m-2,n+1) | D. | (m+2,n-1) |
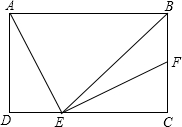 如图,在矩形ABCD中,∠B的平分线交CD于点E,连接AE,EF⊥AE交BC于点F,求证:AE=EF.
如图,在矩形ABCD中,∠B的平分线交CD于点E,连接AE,EF⊥AE交BC于点F,求证:AE=EF.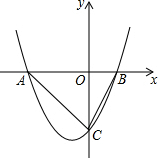 抛物线y=x2+x-2交x轴于点A、B,交y轴于点C,
抛物线y=x2+x-2交x轴于点A、B,交y轴于点C,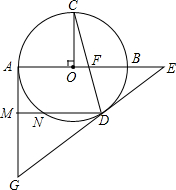 如图,AB为⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的两条切线交于点G,GD交AB延长线于点E,切点为D.
如图,AB为⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的两条切线交于点G,GD交AB延长线于点E,切点为D.