题目内容
18.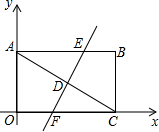 如图,在矩形ABCO中,A点在y轴上,C点在x轴上,A点坐标是(0,4),C点坐标是(8,0),对角线AC的垂直平分线交AB于点E,交AC于点D,交OC于点F.
如图,在矩形ABCO中,A点在y轴上,C点在x轴上,A点坐标是(0,4),C点坐标是(8,0),对角线AC的垂直平分线交AB于点E,交AC于点D,交OC于点F.(1)直接写出AB的长度;
(2)求直线EF的函数解析式;
(3)若点M在直线EF上,则平面内是否存在点N,使得四边形ODMN是菱形?若存在,清求出N点的坐标;若不存在,请说明理由.
分析 (1)根据矩形的性质得到AB=OC,由于A点坐标是(0,4),C点坐标是(8,0),即可求得结果;
(2)直线DE是AC的中垂线,利用待定系数法以及互相垂直的两直线的关系即可求得DE的解析式;
(3)当四边形ODMN是菱形时,OD=DM,求得OD2=42+22=20,由点M在直线EF上,设:M(a,2a-6),根据OD2=DM2,得到20=(a-4)2+[2-(2a-6)]2,求出M1(2,-2),M2(6,6),当M点的坐标为M1(2,-2)时,O(0,0)D(4,2),N1(b,d),由OM的中点与DN1的中点重合,列方程组即可得到结论.
解答 解:(1)∵在矩形ABCO中,
∴AB=OC,AB∥OD,
∵A点坐标是(0,4),C点坐标是(8,0),
∴B(8,4),
∴AB=8;
(2)∵EF垂直平分线AC交AC于D,
∴D为矩形AOCB的中心,
∴D(4,2),
∵EF⊥AC,
∴直线AC的斜率=-$\frac{1}{2}$,直线EF的斜率=2,
设直线EF的解析式为:y=2x+b,
∴2=4×2+b,
∴b=-6,
∴直线EF的函数解析式为:y=2x-6;
(3)当四边形ODMN是菱形时,OD=DM,∴OD2=42+22=20,
∵点M在直线EF上,
∴设:M(a,2a-6),
∴OD2=DM2,即:20=(a-4)2+[2-(2a-6)]2,
解得:a1=2,a2=6,∴M1(2,-2),M2(6,6),
当M点的坐标为M1(2,-2)时,O(0,0)D(4,2),N1(b,d),
∴OM的中点与DN1的中点重合,
∴$\left\{\begin{array}{l}{\frac{0+2}{2}=\frac{4+b}{2}}\\{\frac{0-2}{2}=\frac{2+d}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-2}\\{d=-4}\end{array}\right.$,
∴N1(-2,-4),
当M点的坐标为M2(6,6)时,
∴OM的中点与DN2的中点重合
,∴$\left\{\begin{array}{l}{\frac{0+6}{2}=\frac{4+b}{2}}\\{\frac{0+6}{2}=\frac{2+d}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=2}\\{d=4}\end{array}\right.$,
∴N2(2,4),
综上所述:若点M在直线EF上,则平面内存在点N,使得四边形ODMN是菱形,清N点的坐标为N1(-2,-4),N2(2,4).
点评 本题考查了矩形的性质,求一次函数的解析式,菱形的性质,勾股定理,两直线垂直时斜率满足的关系,线段中点坐标公式,本题对于N的位置的讨论是解第三问的关键.

| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相交或相离 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | (-2,0) | B. | (0,-2) | C. | (1,0) | D. | (0,1) |
 如图所示,在△ABC中:
如图所示,在△ABC中: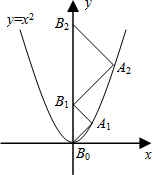 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=2015$\sqrt{2}$.
如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=2015$\sqrt{2}$. 如图,在△ABC中,∠A=40°,∠B=60°,CD是高,CE是角平分线,那么∠DCE=10.
如图,在△ABC中,∠A=40°,∠B=60°,CD是高,CE是角平分线,那么∠DCE=10.