题目内容
5．
如图，在△ABC中，∠A=40°，∠B=60°，CD是高，CE是角平分线，那么∠DCE=10．
分析 先求出∠ACB，利用角平分线得到∠BCE的度数．再由∠B与∠BCD互余求得∠BCD，这样可得到∠DCE．
解答 解：∵在△ABC中，∠A=40°，∠B=60°，
∴∠ACB=180°-∠A-∠B=80°，
∵CE是∠ACB的平分线，
∴∠ECB=$\frac{1}{2}$∠ACB=40°，
∵CD是△ACB的高，
∴∠CDB=90°，
∵∠B=60°，
∴∠DCB=90°-60°=30°，
∴∠DCE=∠ECB-∠DCB=40°-30°=10°，
故答案为：10°．
点评 本题考查了三角形内角和定理，角平分线定义的应用，注意：三角形的内角和等于180°．
练习册系列答案
相关题目
如图，已知△ACO顶点A和C都在双曲线y=$\frac{k}{x}（x＞0）$的一个分支上，延长AC交x轴于点B，过A作AE⊥OB于E，过C作CD⊥OB于D，当E恰为OD中点时，△AOC的面积为6，则k=8．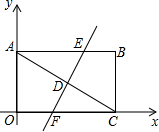
如图，在矩形ABCO中，A点在y轴上，C点在x轴上，A点坐标是（0，4），C点坐标是（8，0），对角线AC的垂直平分线交AB于点E，交AC于点D，交OC于点F．
