Question

20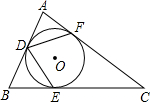．如图，在Rt△ABC中，∠A=90°，∠B=65°，△ABC的内切圆⊙O与边AB，BC，CA分别相切于点D，E，F，则∠FDE的度数为75.5度．

Answer 1

分析 连接OF、OE，根据切线的性质得出∠OFC=∠OEC=90°，根据三角形内角和定理求出∠C，求出∠FOE，根据圆周角定理求出即可．

解答 解：连接OF、OE，

∵在Rt△ABC中，∠A=90°，∠B=65°，
∴∠C=180°-∠A-∠B=25°，
∵⊙O是△ABC的内切圆，
∴∠OFC=∠OEC=90°，
∴∠FOE=360°-∠C-∠OFC-∠OEC=155°，
∴∠FDE=$\frac{1}{2}$∠FOE=75.5°，
故答案为：75.5．

点评 本题考查了三角形内切圆，切线的性质，圆周角定理的应用，能正确作出辅助线是解此题的关键，注意：圆的切线垂直于过切点的半径．