题目内容
8.已知x1,x2为一元二次方程2x2+3x-1=0的两个实数根,那么x12+x22=$\frac{13}{4}$.分析 由根与系数的关系可得“x1+x2=-$\frac{b}{a}$=-$\frac{3}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$”,利用完全平方公式将x12+x22变形为$({x}_{1}+{x}_{2})^{2}$-2x1•x2,代入数据即可得出结论.
解答 解:∵x1,x2为一元二次方程2x2+3x-1=0的两个实数根,
∴x1+x2=-$\frac{b}{a}$=-$\frac{3}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$.
∵x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1•x2,
∴x12+x22=$(-\frac{3}{2})^{2}$-2×(-$\frac{1}{2}$)=$\frac{13}{4}$.
故答案为:$\frac{13}{4}$.
点评 本题考查了根与系数的关系以及完全平方公式,解题的关键是得出“x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$”.本题属于基础题,难度不大,解决该题型题目时,利用根与系数的关系得出两根之和与两根之积是关键.

练习册系列答案
相关题目
18.2015年12月26日,南昌地铁一号线正式开通试运营.据统计,开通首日全天客流量累积近25万人次,数据25万可用科学记数法表示为( )
| A. | 0.25×105 | B. | 2.5×104 | C. | 25×104 | D. | 2.5×105 |
3.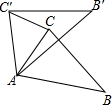 如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 75° |
18.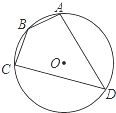 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
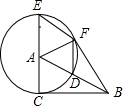 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
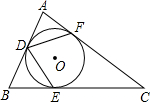 如图,在Rt△ABC中,∠A=90°,∠B=65°,△ABC的内切圆⊙O与边AB,BC,CA分别相切于点D,E,F,则∠FDE的度数为75.5度.
如图,在Rt△ABC中,∠A=90°,∠B=65°,△ABC的内切圆⊙O与边AB,BC,CA分别相切于点D,E,F,则∠FDE的度数为75.5度.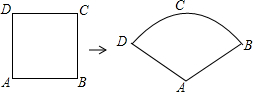 如图,将边长为2的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( )
如图,将边长为2的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( )