题目内容
11.在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
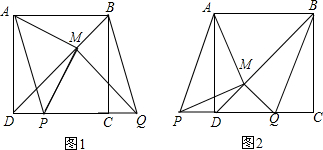
分析 (1)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可;
(2)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可.
解答 解:(1)连接CM,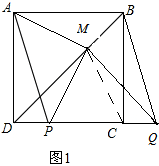
∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中
$\left\{\begin{array}{l}{DM=QM}\\{∠MDP=∠MQC}\\{DP=QC}\end{array}\right.$
∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠AMP=180°-∠ADP=90°,
∴AM=PM,AM⊥PM.
(2)成立,
理由如下:
连接CM,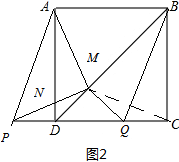
∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中
$\left\{\begin{array}{l}{DM=QM}\\{∠MDP=∠MQC}\\{DP=QC}\end{array}\right.$
∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠DAM=∠MPC,
∵∠PND=∠ANM
∴∠AMP=∠ADP=90°
∴AM=PM,AM⊥PM.
点评 此题是四边形综合题,主要考查了正方形的性质,等腰三角形的性质和判定,垂直的判定方法,解本题的关键是构造全等三角形.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6. 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
3.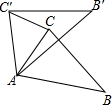 如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 75° |
1.将点A(3,2)沿x轴向左平移4个单位长度,再沿y轴向下平移4个单位长度后得到点A′,则点A′的坐标是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (-1,-2) |
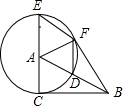 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.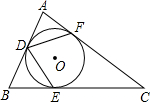 如图,在Rt△ABC中,∠A=90°,∠B=65°,△ABC的内切圆⊙O与边AB,BC,CA分别相切于点D,E,F,则∠FDE的度数为75.5度.
如图,在Rt△ABC中,∠A=90°,∠B=65°,△ABC的内切圆⊙O与边AB,BC,CA分别相切于点D,E,F,则∠FDE的度数为75.5度.