题目内容
4.实数x,y满足(x-$\sqrt{{x}^{2}-2011}$)(y-$\sqrt{{y}^{2}-2011}$)=2011,则x2+3x-3y-2010=( )| A. | -2011 | B. | 2011 | C. | -1 | D. | 1 |
分析 由已知等式变形得出x、y的关系,再将所求式子化简求值即可.
解答 解:把(x-$\sqrt{{x}^{2}-2011}$)(y-$\sqrt{{y}^{2}-2011}$)=2011,两边同乘(x-$\sqrt{{x}^{2}-2011}$)得:
$\sqrt{{x}^{2}-2011}$+$\sqrt{{y}^{2}-2011}$)=y-x,
把(x-$\sqrt{{x}^{2}-2011}$)(y-$\sqrt{{y}^{2}-2011}$)=2011,两边同乘(y-$\sqrt{{y}^{2}-2011}$)得:
$\sqrt{{x}^{2}-2011}$+$\sqrt{{y}^{2}-2011}$)=x-y,
则$\sqrt{{x}^{2}-2011}$+$\sqrt{{y}^{2}-2011}$=0,
解得:x2=2011,x-y=0,
代入原式=2011-3(x-y)-2010=1;
故选D.
点评 此题考查了二次根式的化简求值,关键是根据题意求出x2与x-y的值.

练习册系列答案
相关题目
2.小明从一副扑克中随机摸1张牌,下列事件中,不属于等可能事件的是( )
| A. | 摸到大王与摸到小王 | B. | 摸到红桃与摸到黑桃 | ||
| C. | 摸到点5与摸到点6 | D. | 摸到点5与摸到王牌 |
16.若∠1=15°12′,∠2=15.3°,∠3=15°18′,则( )
| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | 以上均不对 |
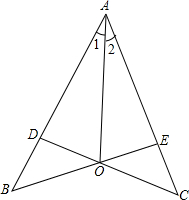 如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.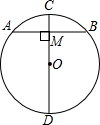 如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?
如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?