题目内容
11. 如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为$\widehat{AB}$的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2cm2.
如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为$\widehat{AB}$的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2cm2.
分析 连接OC、EC,由△OCD≌△OCE、OC⊥DE可得DE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD-S△ODE=S阴影部分可得.
解答 解:连结OC,过C点作CF⊥OA于F,
∵半径OA=4,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2
| 2 |
∴空白图形ACD的面积=扇形OAC的面积-三角形OCD的面积
=
| 45π×42 |
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
三角形ODE的面积=
| 1 |
| 2 |
∴图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积
=
| 90π×42 |
| 360 |
| 2 |
=2π+2
| 2 |
故答案为:2π+2
| 2 |
点评 本题主要考查扇形面积的求法,熟知并理解扇形面积计算公式是基础,利用割补法求扇形面积是常用作法,解题的关键是如何添加辅助线来有效割补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若点P(13,y)第二象限,则y的取值范围是( )
| A. | y<0 | B. | y≤0 | C. | y>0 | D. | y≥0 |
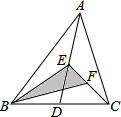 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.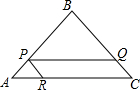 已知:如图,Rt△ABC中,∠B=90°,AB=BC=8cm,P为AB上任意一点,PR∥BC,PQ∥AC,S?PQCR=16cm2,求AP的长.
已知:如图,Rt△ABC中,∠B=90°,AB=BC=8cm,P为AB上任意一点,PR∥BC,PQ∥AC,S?PQCR=16cm2,求AP的长. 端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.
端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.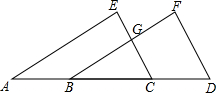 如图,已知:如图,EC∥FD,∠F=∠E,点A,B,C,D在一条直线上,EA与FB有怎样的位置关系?为什么?
如图,已知:如图,EC∥FD,∠F=∠E,点A,B,C,D在一条直线上,EA与FB有怎样的位置关系?为什么?