题目内容
17.某校在一次迎“六一”的活动中,学们要用彩纸折3000只纸鹤装饰礼堂,但在原定参加折纸鹤的同学中,有10名同学因为要排练节目而没有参加,这样折纸鹤的同学平均每人折的数量比原定的同学平均每人要完成的数量多15只,问原定共有多少同学要折纸鹤?分析 设原定有x名同学要折纸鹤,然后根据这样折纸鹤的同学平均每人折的数量比原定的同学平均每人要完成的数量多15只列方程求解即可.
解答 解:设原定有x名同学要折纸鹤.
根据题意得:$\frac{3000}{x}$+15=$\frac{3000}{x-10}$,
解得:x1=50,x2=-40(舍去).
当x=50时,x(x-10)≠0.
所以x=50是原方程得解.
答:原定有50名同学要折纸鹤.
点评 本题主要考查的是分式方程的应用,根据题意列出关于x的方程是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7.某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线AB外一点M,作一直线垂直于直线AB”,各自提供了如下四种方案,其中正确的是( )
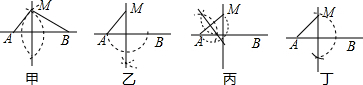
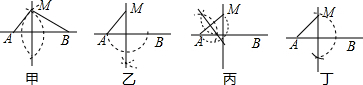
| A. | 甲、乙 | B. | 乙、丙 | C. | 丙、丁 | D. | 甲、乙、丙 |
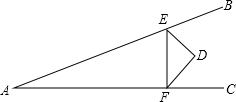 如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.
如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数. 如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长.
如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长.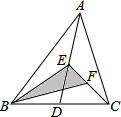 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3. 如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°.
如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°.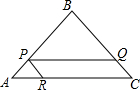 已知:如图,Rt△ABC中,∠B=90°,AB=BC=8cm,P为AB上任意一点,PR∥BC,PQ∥AC,S?PQCR=16cm2,求AP的长.
已知:如图,Rt△ABC中,∠B=90°,AB=BC=8cm,P为AB上任意一点,PR∥BC,PQ∥AC,S?PQCR=16cm2,求AP的长.