题目内容
10.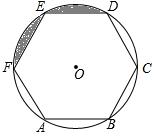 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.(1)求$\widehat{AB}$的长;
(2)求阴影部分的面积.
分析 (1)连接OE、OA、OF、OB,求出中心角则∠AOF=∠EOF=∠AOB=60°,得出∠BOE=180°,由弧长公式即可得出结果;
(2)连接OD,证明△DOE,△EOF是等边三角形,求出△△EOF的面积=△DOE的面积=$\frac{\sqrt{3}}{4}$,由扇形面积公式求出扇形DOF的面积的面积,即可求出阴影部分的面积.
解答 解: (1)连接OE、OA、OF、OB,如图1所示:
(1)连接OE、OA、OF、OB,如图1所示:
则∠AOF=∠EOF=∠AOB=60°,
∴∠BOE=180°,
∴$\widehat{AB}$的长=$\frac{180π×1}{180}$=π;
(2)连接OD,如图2所示:
则∠DOE=∠EOF=60°,
∵OD=OE=OF,
∴△DOE,△EOF是等边三角形,
∴△△EOF的面积=△DOE的面积=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,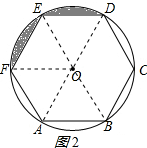
∵扇形DOF的面积=$\frac{120π×{1}^{2}}{360}$=$\frac{1}{3}$π,
∴阴影部分的面积=$\frac{1}{3}$π-2×$\frac{\sqrt{3}}{4}$=$\frac{π}{3}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查了正多边形的性质、等边三角形的判定与性质、弧长公式、扇形面积公式;熟练掌握正六边形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
1.若点P(13,y)第二象限,则y的取值范围是( )
| A. | y<0 | B. | y≤0 | C. | y>0 | D. | y≥0 |
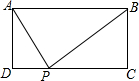 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5. 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )



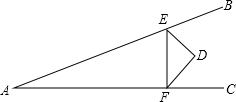 如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.
如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.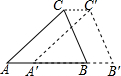 如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.
如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.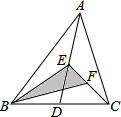 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.