题目内容
8. 如图在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则△BDE的面积为( )
如图在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则△BDE的面积为( )| A. | $\frac{75}{4}$ | B. | $\frac{21}{4}$ | C. | 21 | D. | 24 |
分析 先根据矩形的性质得AB=CD=6,AD=BC=8,AD∥BC,再根据折叠的性质得∠DBC=∠DBE,由AD∥BC得∠DBC=∠BDE,所以∠BDE=∠EBD,根据等腰三角形的判定得EB=ED,设ED=x,则EB=x,AE=8-x,在Rt△ABE根据勾股定理得到62+(8-x)2=x2,求出x的值,然后根据三角形面积公式求解即可.
解答 解:∵四边形ABCD为矩形,
∴AB=CD=6,AD=BC=8,AD∥BC,
∵矩形纸片ABCD沿对角线BD折叠,点C落在点E处,
∴∠DBC=∠DBE,
∵AD∥BC,
∴∠DBC=∠BDE,
∴∠BDE=∠EBD,
∴EB=ED,
设ED=x,则EB=x,AE=8-x,
在Rt△ABE中,∵AB2+AE2=BE2,
∴62+(8-x)2=x2,
解得x=$\frac{25}{4}$,
∴DE=$\frac{25}{4}$,
∴△BDE的面积=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×6×$\frac{25}{4}$=$\frac{75}{4}$.
故选A.
点评 本题考查了矩形的性质、勾股定理的运用以及折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
16. 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )
 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )| A. | ∠ABD=∠BDC | B. | AC⊥BD | C. | AB=CD | D. | ∠BAD=∠BCD |
13. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
18.已知直线a、b、c在同一平面内,则下列说法错误的是( )
| A. | 如果a∥b,b∥c,那么a∥c | |
| B. | a⊥b,c⊥b,那么a∥c | |
| C. | 如果a与b相交,b与c相交,那么a与c一定相交 | |
| D. | 如果a与b相交,b与c不相交,那么a与c一定相交 |
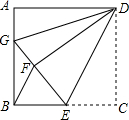 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,则BG=8.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,则BG=8.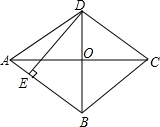 如图,菱形ABCD的两条对角线相交于点O,若AC=24,BD=10,过点D作DE⊥AB,垂足为E,则DE的长是$\frac{120}{13}$.
如图,菱形ABCD的两条对角线相交于点O,若AC=24,BD=10,过点D作DE⊥AB,垂足为E,则DE的长是$\frac{120}{13}$. 如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°.
如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°. 如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第2n次跳动至A2n坐标(n+1,n).
如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第2n次跳动至A2n坐标(n+1,n).