题目内容
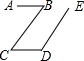
16．
如图，在平行四边形ABCD中，下列结论错误的是（ ）| A． | ∠ABD=∠BDC | B． | AC⊥BD | C． | AB=CD | D． | ∠BAD=∠BCD |
分析 由平行四边形的性质容易得出结论．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，∠BAD=∠BCD，OA=OC，OB=OD，
∴∠ABD=∠BDC，
∴选项A、C、D正确，选项B错误；
故选：B．
点评 本题考查了平行四边形的性质；熟记平行四边形的性质是解决问题的关键．
练习册系列答案
相关题目
6．下列根式中属最简二次根式的是（ ）
| A． | $\sqrt{{a^2}+1}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{3{a^2}b}$ | D． | $\sqrt{9x}$ |
7．下列叙述中，正确的是（ ）
| A． | 在同一平面内，两条直线的位置关系有三种，分别是相交、平行、垂直 | |
| B． | 不相交的两条直线叫平行线 | |
| C． | 两条直线的铁轨是平行的 | |
| D． | 我们知道，对顶角是相等的，那么反过来，相等的角就是对顶角 |
按要求完成下列证明
11．
如图，能判定AD∥BC的条件是（ ）
如图，能判定AD∥BC的条件是（ ）| A． | ∠3=∠2 | B． | ∠1=∠2 | C． | ∠B=∠D | D． | ∠B=∠1 |
1．
如图，在平面直角坐标系中，三角形ABC的三个顶点的坐标分别为A（-2，5）、B（-4，3）、C（-1，1），请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1，并求出三角形ABC的面积．
如图，在平面直角坐标系中，三角形ABC的三个顶点的坐标分别为A（-2，5）、B（-4，3）、C（-1，1），请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1，并求出三角形ABC的面积．
8．
如图在矩形ABCD中，BC=8，CD=6，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则△BDE的面积为（ ）
如图在矩形ABCD中，BC=8，CD=6，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则△BDE的面积为（ ）| A． | $\frac{75}{4}$ | B． | $\frac{21}{4}$ | C． | 21 | D． | 24 |