Question

3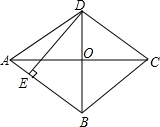．如图，菱形ABCD的两条对角线相交于点O，若AC=24，BD=10，过点D作DE⊥AB，垂足为E，则DE的长是$\frac{120}{13}$．

Answer 1

分析 直接利用菱形的性质得出其边长，再利用菱形面积求法得出DE的长．

解答 解：∵菱形ABCD的两条对角线相交于点O，AC=24，BD=10，
∴AO=CO=12，DO=BO=5，AC⊥BD，
∴AB=13，
∴$\frac{1}{2}$AC•BD=13×DE，
则$\frac{1}{2}$×24×10=13•DE，
解得：DE=$\frac{120}{13}$．
故答案为：$\frac{120}{13}$．

点评 此题主要考查了菱形的性质，得出菱形的边长是解题关键．