题目内容
15．
如图，线段AB和A1B1线段成中心对称图形（A、B的对称点分别是A1、B1）．在图中用尺规（不写作法，保留作图痕迹）．（1）作线段AB和A1B1线段的对称中心O；
（2）作△ABC关于点O的中心对称图形．
分析 （1）连接AA1和BB1，它们的交点为O点；
（2）延长CO到C1，使C1O=CO，然后连接B1C1、A1C1，则△A1B1C1为满足条件．
解答 解：（1）如图，点O即为所求作的对称中心；
（2）如图，△A1B1C1即为△ABC关于点O的中心对称图形．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．
如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=40°，则∠2=（ ）
如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=40°，则∠2=（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 60° |
20．在-1.414，$\frac{22}{7}$，$\root{3}{-27}$，$\frac{π}{3}$，-$\sqrt{2}$，3.14，$\sqrt{9}$，0.1212212221…（两个1之间依次多1个2）中，无理数的个数是（ ）
| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
4．把$\frac{{-\sqrt{45{y^2}}}}{{3\sqrt{5y}}}$化简后得（ ）
| A． | $\frac{{-\sqrt{9y}}}{3}$ | B． | $-\sqrt{y}$ | C． | $-3\sqrt{5y}$ | D． | $\frac{{3\sqrt{5}}}{5}$ |
5．
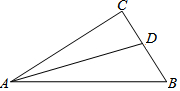如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）
如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）| A． | 48 | B． | 50 | C． | 54 | D． | 60 |