题目内容
19.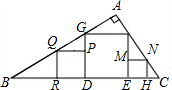 如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系.
如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系.
分析 因为Rt△ABC内有边长分别为a、b、c的三个正方形,所以图中三角形都相似,且与a、b、c关系密切的是△DHE和△GQF,只要它们相似即可得出所求的结论.
解答 解:如图,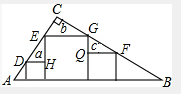
∵DH∥AB∥QF
∴∠EDH=∠A,∠GFQ=∠B;
又∵∠A+∠B=90°,∠EDH+∠DEH=90°,∠GFQ+∠FGQ=90°;
∴∠EDH=∠FGQ,∠DEH=∠GFQ;
∴△DHE∽△GQF,
∴$\frac{DH}{GQ}=\frac{EH}{FQ}$,
∴$\frac{a}{b-c}$=$\frac{b-a}{c}$,
∴ac=(b-c)(b-a)
∴b2=ab+bc=b(a+c),
∴b=a+c.
点评 此题考查了相似三角形的判定和性质,直角三角形的性质,正方形的性质,熟练掌握三角形的判定和性质定理是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,将矩形沿图中虚线(其中x>y)剪成①②③④四块图形,用这四块图形恰能拼成一个正方形,若x=4,则y=2$\sqrt{5}$-2.
如图,将矩形沿图中虚线(其中x>y)剪成①②③④四块图形,用这四块图形恰能拼成一个正方形,若x=4,则y=2$\sqrt{5}$-2.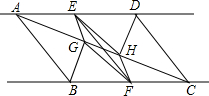 如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.
如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分. 写出图中直线所对应的函数关系.
写出图中直线所对应的函数关系. 如图,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,垂足为D、E,试说明DE=$\frac{1}{2}$BC.
如图,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,垂足为D、E,试说明DE=$\frac{1}{2}$BC.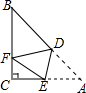 如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).
如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).