题目内容
17．若m是不等式组$\left\{\begin{array}{l}{2（1-x）＜x+8}\\{\frac{3x-2}{6}＜\frac{x-1}{3}}\end{array}\right.$的最大整数解，求1+m+m2+…+m2014．分析 先求出每个不等式的解集，再求出不等式组的解集，求出最大整数解，代入求出即可．
解答 解：$\left\{\begin{array}{l}{2（1-x）＜x+8①}\\{\frac{3x-2}{6}＜\frac{x-1}{3}②}\end{array}\right.$，
∵解不等式①得：x＞-2，
解不等式②得：x＜0，
∴不等式组的解集为-2＜x＜0，
∴不等式组的最大整数解为-1，
∴1+m+m2+…+m2014
=1+（-1）+（-1）2+（-1）3+…+（-1）2014
=1
点评 本题考查了解一元一次不等式，解一元一次不等式组，不等式组的整数解的应用，解此题的关键是求出不等式组的最大整数解，难度适中．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
7．
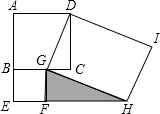如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（ ）
如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（ ）| A． | 10 | B． | 11 | C． | $\frac{15}{2}$ | D． | $\frac{45}{4}$ |
5．
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）| A． | 4$\sqrt{5}$-4 | B． | 4$\sqrt{7}$-4 | C． | 8$\sqrt{2}$-4 | D． | 8-2$\sqrt{2}$ |
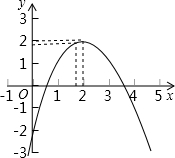已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0；②9a+4b+c＜0；③9a-c+1＞0；④a＜-$\frac{1}{8}$，其中，正确的结论的个数是（ ）
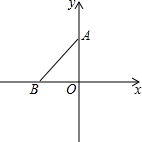如图，在直角坐标平面内有两点A（0，2）、B（-2，0），且A、B两点之间的距离等于a（a为大于0的已知数），在不计算a的数值的条件下，完成下列问题：