题目内容
9.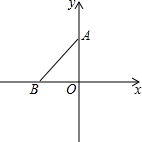 如图,在直角坐标平面内有两点A(0,2)、B(-2,0),且A、B两点之间的距离等于a(a为大于0的已知数),在不计算a的数值的条件下,完成下列问题:
如图,在直角坐标平面内有两点A(0,2)、B(-2,0),且A、B两点之间的距离等于a(a为大于0的已知数),在不计算a的数值的条件下,完成下列问题:(1)以学过的只是用一句话说出a>2的理由;
(2)在x轴上是否存在点P,使△PAB是等腰三角形?如果存在,请写出点P的坐标,并求出△PAB的面积;如果不存在,请说明理由.
分析 (1)利用直角三角形三边关系可得出结论;
(2)利用等腰直角三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
解答 解:(1)∵AO=BO,∠AOB=90°,
∴AB>2,
∴a>2的理由直角三角形斜边大于直角边;
(2)存在三种:
若AP=BP,则 P(0,0),面积2×2÷2=2;
若BP=BA,则P(-a-2,0),面积a×2÷2=a;
若BA=AP,则P (2,0),面积4×2÷2=4.
点评 本题主要考查了等腰直角三角形的判定和性质,分类讨论是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.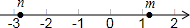 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
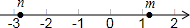 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |
3.现有A、B两家粮食种植基地往甲、乙两个粮食配送中心运送粮食,A地可运出粮食80吨,B地可运出粮食60吨,其中甲地需要粮食90吨,乙地需要粮食50吨,每吨粮食运费如下:从A基地运往甲、乙两中心的运费分别为每吨500元和400元,从B基地运往甲、乙两中心的运费分别为每吨200元和300元.设A地运送到甲中心粮食为x吨
(1)请根据题意填写下表(填写表中所有空格):
(2)若某次运送总运费共花去50000元,请指出当时的调运方案;
(3)按照题(2)的调运方案,从A基地往甲中心运送粮食,在运输途中的E地接到F地商家的一个电话,该商家需要25吨.已知A基地与E地之间的运费为每吨520元,甲中心与F地之间的运费为每吨480元.现A基地有两种方案运送到甲中心和F地商家:
方案一:从E地直接运送到F地商家,运到后把剩下的粮食运到甲中心;
方案二:先把粮食运到甲中心,再运25吨到F地商家.
若方案一比方案二的总运费多21000元,则从E地到F地商家的运费是每吨多少元?
(1)请根据题意填写下表(填写表中所有空格):
| 运往甲地 | 运往乙地 | |
| A | ||
| B |
(3)按照题(2)的调运方案,从A基地往甲中心运送粮食,在运输途中的E地接到F地商家的一个电话,该商家需要25吨.已知A基地与E地之间的运费为每吨520元,甲中心与F地之间的运费为每吨480元.现A基地有两种方案运送到甲中心和F地商家:
方案一:从E地直接运送到F地商家,运到后把剩下的粮食运到甲中心;
方案二:先把粮食运到甲中心,再运25吨到F地商家.
若方案一比方案二的总运费多21000元,则从E地到F地商家的运费是每吨多少元?
 为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.
为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.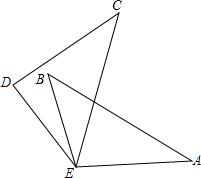 如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.
如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.