题目内容
6.已知2a-1的平方根是±3,3a+b-1的立方根是4,求5a+4b的平方根.分析 首先根据2a-1的平方根是±3,可得2a-1=32=9,据此求出a的值是多少;然后根据3a+b-1的立方根是4,可得3a+b-1=43=64,据此求出b的值是多少;最后用5a加上4b,求出5a+4b的值是多少,进而求出5a+4b的平方根是多少即可.
解答 解:∵2a-1的平方根是±3,
∴2a-1=32=9,
解得a=5;
∵3a+b-1的立方根是4,
∴3a+b-1=43=64,
∴3×5+b-1=64,
解得b=50;
∴5a+4b
=5×5+4×50
=25+200
=225
∵(±15)2=225,
∴5a+4b的平方根是±15.
点评 (1)此题主要考查了立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.
(2)此题还考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.计算$\sqrt{\frac{b}{a}}$÷$\sqrt{ab}$×$\sqrt{\frac{1}{ab}}$(a>0,b>0)的值为( )
| A. | $\frac{1}{a{b}^{2}}$$\sqrt{ab}$ | B. | $\frac{1}{{a}^{2}b}$$\sqrt{ab}$ | C. | $\frac{1}{b}\sqrt{ab}$ | D. | b$\sqrt{ab}$ |
11.若两条平行直线被第三条直线所截,则( )
| A. | 一对同旁内角的角平分线互相垂直 | B. | 一对内错角的角平分线互相垂直 | ||
| C. | 一对同位角的角平分线互相垂直 | D. | 以上都不对 |
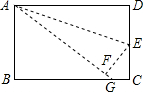 如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.
如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.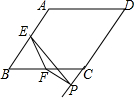 如图,在菱形ABCD中,∠A=130°.E,F分别是边AB和BC的中点,EP⊥CD,交DC的延长线于点P.则∠FPC=115°.
如图,在菱形ABCD中,∠A=130°.E,F分别是边AB和BC的中点,EP⊥CD,交DC的延长线于点P.则∠FPC=115°.