题目内容
18.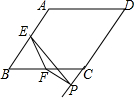 如图,在菱形ABCD中,∠A=130°.E,F分别是边AB和BC的中点,EP⊥CD,交DC的延长线于点P.则∠FPC=115°.
如图,在菱形ABCD中,∠A=130°.E,F分别是边AB和BC的中点,EP⊥CD,交DC的延长线于点P.则∠FPC=115°.
分析 延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPM的度数,即可求出答案.
解答 解:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠GBF=∠PCF,
∵E,F分别是边AB和BC的中点,
∴BF=CF,AE=BE,
∵AB∥CD,PE⊥AB,
∴PE⊥CD,
∴∠BEP=∠EPC=∠EPM=90°,
延长PF交AB于点G,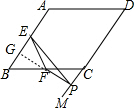
在△BGF与△CPF中,
$\left\{\begin{array}{l}{∠GBF=∠PCF}\\{BF=CF}\\{∠BFG=∠CFP}\end{array}\right.$
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点,
又∵EP⊥CD,
∴∠BEP=90°,
∴EF=$\frac{1}{2}$PG(直角三角形斜边上的中线等于斜边的一半),
∵PF=$\frac{1}{2}$PG(中点定义),
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPM=90°,
∴∠BEP-∠FEP=∠EPM-∠EPF,即∠BEF=∠FPM,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=50°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=$\frac{1}{2}$(180°-50°)=65°,
∴∠FPM=65°,
∴∠FPC=180°-65°=115°,
故答案为:115°.
点评 此题主要考查了菱形的性质的理解及运用,灵活应用菱形的性质是解决问题的关键,注意:菱形的对边平行,菱形的四条边相等.

练习册系列答案
相关题目
3.如果a=(-99)0,b=(-0.1)-1,C=($-\frac{5}{3}$)-2,那么a、b、c的大小关系为( )
| A. | a>c>b | B. | c>a>b | C. | a>b>c | D. | c>b>a |
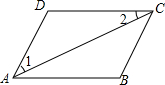 如图,AC平分∠DAB,∠1=∠2,请结合图形填空:
如图,AC平分∠DAB,∠1=∠2,请结合图形填空: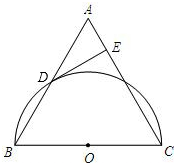 已知△ABC是等边三角形,以BC为直径的半圆O与边AB相交于点D,DE⊥AC,垂足为点E.
已知△ABC是等边三角形,以BC为直径的半圆O与边AB相交于点D,DE⊥AC,垂足为点E.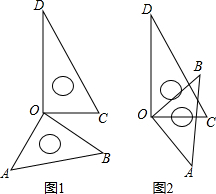 (1)如图1所示,将一副三角尺的直角顶点重合在点O处.
(1)如图1所示,将一副三角尺的直角顶点重合在点O处.