题目内容
16.3$\sqrt{2}$-2$\sqrt{2}$=2$\sqrt{2}$,$\sqrt{3}$($\sqrt{3}$+$\frac{1}{\sqrt{3}}$)=4,$\root{3}{5}$+|-$\root{3}{5}$|=2$\root{3}{5}$.分析 根据实数的运算分别合并同类二次根式、乘法分配律及二次根式乘法、绝对值性质及合并同类二次根式.
解答 解:3$\sqrt{2}$-2$\sqrt{2}$=(3-2)×$\sqrt{2}$=2$\sqrt{2}$;
$\sqrt{3}$($\sqrt{3}$+$\frac{1}{\sqrt{3}}$)=$\sqrt{3}$×$\sqrt{3}$+$\sqrt{3}$×$\frac{1}{\sqrt{3}}$=3+1=4;
$\root{3}{5}$+|-$\root{3}{5}$|=$\root{3}{5}$+$\root{3}{5}$=2$\root{3}{5}$;
故答案为:2$\sqrt{2}$,4,2$\root{3}{5}$.
点评 本题主要考查实数的运算,熟练掌握二次根式的运算法则是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.关于x的方程(m-3)x${\;}^{{m}^{2}-2m-1}$-mx+6=0是一元二次方程,则它的一次项系数是( )
| A. | -1 | B. | 1 | C. | 3 | D. | 3或-1 |
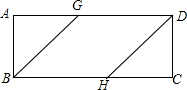 在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为1+$\sqrt{2}$.
在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为1+$\sqrt{2}$.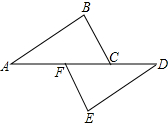 如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.
如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.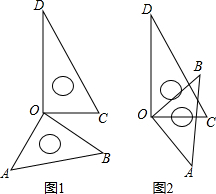 (1)如图1所示,将一副三角尺的直角顶点重合在点O处.
(1)如图1所示,将一副三角尺的直角顶点重合在点O处.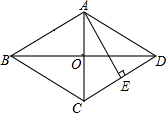 如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数.
如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数.