题目内容
18.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.(1)根据题意,填写下列表格;
| 时间(s) | 0 | 5 | 7 | x |
| A点位置 | 19 | -1 | -9 | -4x+19 |
| B点位置 | -8 | 17 | 27 | 5x-8 |
(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.
分析 (1)根据两点之间的距离,从而可填写表格;
(2)根据相遇的相等关系,得出方程,求解即可;
(3)根据两种情况分别得出方程求解即可.
解答 解:(1)填表如下:
| 时间(s) | 0 | 5 | 7 | x |
| A点位置 | 19 | -1 | -9 | -4x+19 |
| B点位置 | -8 | 17 | 27 | 5x-8 |
解得:x=3.
答:相遇的时刻为3秒,在数轴上的位置为7;
(3)根据题意可得:-4x+19-(5x-8)=18
解得:x=1;
根据题意可得:5x-8-(-4x+19)=18
解得:x=5.
综上所述,x=1或5时,A、B两点能否相距18个单位长度.
点评 本题考查了一元一次方程的应用,解答本题的关键是表示出x小时时,两点的位置,注意利用方程思想的求解,有一定难度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8. 对于抛物线y=x2+4x+3
对于抛物线y=x2+4x+3
(1)它与x轴交点的坐标为(-1,0)和(-3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
(3)结合图象回答问题:当-3<x<0时,y的取值范围是-1<y<3.
 对于抛物线y=x2+4x+3
对于抛物线y=x2+4x+3(1)它与x轴交点的坐标为(-1,0)和(-3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
| x | … | … | |||||
| y | … | … |
6.下列合并同类项正确的有( )
| A. | 2a+4a=8a2 | B. | 3x+2y=5xy | C. | 7x2-3x2=4 | D. | 9a2b-9ba2=0 |
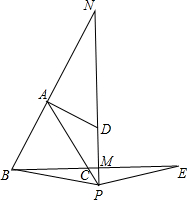 已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.
已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.