题目内容
1.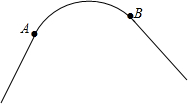 如图,一条公路的转弯处是一段圆弧AB.
如图,一条公路的转弯处是一段圆弧AB.(1)作出AB所在圆的圆心O;
(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)若弧AB的中点C到弦AB的距离为20m,AB=80m,求AB所在圆径.
分析 (1)根据圆的概念和线段垂直平分线的性质作图;
(2)根据垂径定理求出AH的长,根据勾股定理计算即可.
解答 解(1)如图1,
在圆弧AB上任取一点D,分别作AB、AD的中垂线于交O,
则点O即为所求.
(2)如图2,
设圆弧AB所在圆的半径为r,则AO=r,OH=r-20,
∵OC⊥AB,
∴AH=$\frac{1}{2}$AB=40,
∴在Rt△AHO中,由勾股定理得:402+(r-20)2=r2,
∴r=50m.
点评 本题考查的是垂径定理的应用、尺规作图以及勾股定理的应用,掌握尺规作图的一般步骤和垂径定理是解题的关键.

练习册系列答案
相关题目
6.下列合并同类项正确的有( )
| A. | 2a+4a=8a2 | B. | 3x+2y=5xy | C. | 7x2-3x2=4 | D. | 9a2b-9ba2=0 |
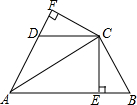 已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.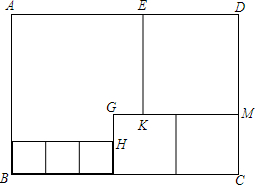 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm.
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm.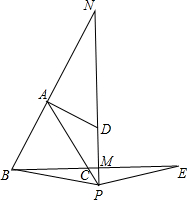 已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.
已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.