题目内容
 如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.
如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:连接DE,DF,易证∠B=∠C,即可证明△BDE≌△CFD,可得DE=DF,根据等腰三角形底边三线合一的性质即可解题.
解答:证明:连接DE,DF,

∵AB=AC,∴∠B=∠C,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(SAS),
∴DE=DF,
∵DG⊥EF,
∴EG=FG.

∵AB=AC,∴∠B=∠C,
在△BDE和△CFD中,
|
∴△BDE≌△CFD(SAS),
∴DE=DF,
∵DG⊥EF,
∴EG=FG.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等腰三角形底边三线合一的性质,本题中求证△BDE≌△CFD是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D.
如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D. 已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y=
已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y= 用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段a,c,∠α.
用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段a,c,∠α. 如图,∠AOB=60°,∠AOC=90°,OB是∠AOD的平分线,求∠COD的度数.
如图,∠AOB=60°,∠AOC=90°,OB是∠AOD的平分线,求∠COD的度数.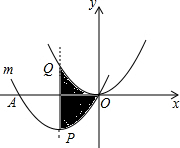 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为
如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为