题目内容
20.已知:(x+y)2=12,(x-y)2=6,求下列代数式的值:(1)x2+y2;
(2)x2+3xy+y2.
分析 已知等式利用完全平方公式化简,整理后即可求出所求式子的值.
解答 解:∵(x+y)2=12,(x-y)2=6,
∴x2+2xy+y2=12①,x2-2xy+y2=6②,
(1)①+②得:2(x2+y2)=18,即x2+y2=9;
(2)①-②得:4xy=6,即xy=$\frac{3}{2}$,
则原式=9+3×$\frac{3}{2}$=$\frac{27}{2}$.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
2. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 55° | B. | 50° | C. | 45° | D. | 60° |
8.若点A(2,n)在x 轴上,则点B(n-2,n+l)在( )
| A. | 第一象限 | B. | 第三象限 | C. | 第四象限 | D. | 第二象限 |
10.(1)根据图示规律填表:

(2)猜想:第n个图形共有多少个正方形?

| 图形编号 | 1×1的正方形个数 | 2×2的正方形个数 | 3×3的正方形个数 | 4×4的正方形个数 |
| ① | ||||
| ② | ||||
| ③ | ||||
| ④ |
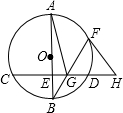 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.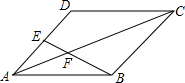 已知平行四边形ABCD中,点E为AD的中点,连接BE交AC于点F.求AF:CF的值.
已知平行四边形ABCD中,点E为AD的中点,连接BE交AC于点F.求AF:CF的值. 如图,已知抛物线与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C(0,5).
如图,已知抛物线与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C(0,5).