题目内容
15.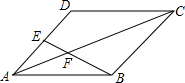 已知平行四边形ABCD中,点E为AD的中点,连接BE交AC于点F.求AF:CF的值.
已知平行四边形ABCD中,点E为AD的中点,连接BE交AC于点F.求AF:CF的值.
分析 根据四边形ABCD是平行四边形,证出△AEF∽△BCF,然后利用其对应边成比例即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴△AEF∽△BCF,
∴$\frac{AE}{BC}=\frac{AF}{CF}$,
∵点E为AD的中点,
∴AE=$\frac{1}{2}$AD-$\frac{1}{2}$BC,
∴$\frac{AF}{CF}=\frac{AE}{BC}$=$\frac{1}{2}$.
点评 此题主要考查学生对相似三角形的判定与性质,平行四边形的性质等知识点,难度不大,属于基础题.

练习册系列答案
相关题目
17.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0,剩余部分沿虚线又剪开拼成一个长方形(不重叠无缝隙),则长方形的周长为( )cm.


| A. | 2a+5 | B. | 4a+10 | C. | 4a+16 | D. | 6a+15 |
7.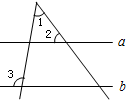 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )
如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )
 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )
如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )| A. | 35° | B. | 45° | C. | 50° | D. | 55° |




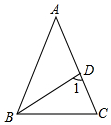 如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC,则∠1的度数是72°.
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC,则∠1的度数是72°.