题目内容
6．
如图，一棵树在一次强台风中，从离地面3米折断，量得倒下部分树尖与树根的距离是4米，这棵树在折断前的高度是（ ）| A． | 7米 | B． | 8米 | C． | 9米 | D． | 10米 |
分析 先根据勾股定理求出大树折断部分的高度，再根据大树的高度等于折断部分的长与未断部分的和即可得出结论．
解答 
解：如图所示：
∵△ABC是直角三角形，AB=3m，AC=4m，
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5（m），
∴大树的高度=AB+AC=3+5=8（m）．
故选：B．
点评 本题考查的是勾股定理的应用，解答此题的关键是先根据勾股定理求出BC的长度，再根据大树的高度=AB+AC进行解答．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，以BC为半径作⊙B，交AB于点D，交AB的延长线于点E，连接CD、CE．
1．下列四个实数中最大的是（ ）
| A． | -5 | B． | 0 | C． | $\root{3}{27}$ | D． | $\sqrt{16}$ |
11．若关于x的一元二次方程x2-2x+m=0有两个不相等的实数根，则m的取值范围是（ ）
| A． | m＞1 | B． | m＞-1 | C． | m＜1 | D． | m＜-1 |
18．已知方程7x+2=3x-6与x-1=k的解相同，则3k2-1的值为（ ）
| A． | 18 | B． | 20 | C． | 26 | D． | -26 |
15．
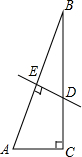如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=8cm，则AC等于（ ）
如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=8cm，则AC等于（ ）| A． | 8cm | B． | 6cm | C． | 4cm | D． | 2.5cm |