题目内容
9.(1)通过计算几何图形的面积可以表示一些代数恒等式,甲图是边长为x的正方形,请用两种不同的方法表示甲图中阴影部分的面积(a,b为常数)①因式的积的形式:(x-a)(x-b);②关于x的二次多项式的形式:x2-(a+b)x+ab;
由①与②,可以得到一个等式:(x-a)(x-b)=x2-(a+b)x+ab
(2)由(1)的结果进行应用:若(a-m)(a-2)=a2+na+6对a的任何值都成立,求m,n的值
(3)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,乙图表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据乙图中图形的变化关系,利用整式乘法写出一个代数恒等式.
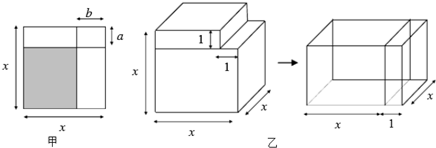
分析 (1)先求得阴影部分矩形的长与宽可直接求得阴影部分的面积,然后依据阴影部分的面积=正方形的面积-1个边长分别为a、x的矩形-1个边长分别为b、x的矩形+一个边长分别为a、b的矩形,从而得到恒等式;
(2)依据(1)的结果可知(a-m)(a-2)=a2-(m+2)a+2m,然后根据两个多项式的对应项相同求解即可;
(3)分别求得图中几何体的体积,然后根据原图形与新图形体积相等列出恒等式即可.
解答 解:(1)①阴影部分的面积=(x-a)(x-b),②阴影部分的面积=x2-ax-bx+ab=x2-(a+b)x+ab,
∵阴影部分的面积不变,
∴(x-a)(x-b)=x2-(a+b)x+ab.
故答案为:①(x-a)(x-b);②x2-(a+b)x+ab;(x-a)(x-b)=x2-(a+b)x+ab.
(2)由(1)可知:(a-m)(a-2)=a2-(m+2)a+2m,
又∵(a-m)(a-2)=a2+na+6,
∴2m=6,n=-(m+2).
解得:m=3,n=-5.
(3)∵原几何体的体积=x3-1×1•x=x3-x,新几何体的体积=(x+1)(x-1)x,
∴x3-x=(x+1)(x-1)x.
点评 本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
1.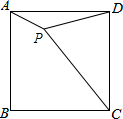 如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )
如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )
 如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )
如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
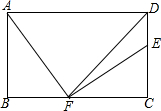 如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.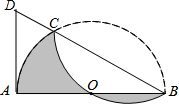 已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.
已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.