题目内容
3. 如图,已知$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$,则:
如图,已知$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$,则:①$\frac{CE}{AE}$=$\frac{5}{2}$;
②若BD=10cm,则AD=4cm.
③若△ADE的周长为16cm,则△ABC的周长为24cm.
分析 ①由比例的性质即可得出结果;
②由比例的性质即可得出结果;
③与已知条件证出△ABC∽△ADE,由相似三角形的性质即可得出结果.
解答 解:①∵$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$=$\frac{3}{2}$,
∴$\frac{CE}{AE}$=$\frac{5}{2}$;
故答案为:$\frac{5}{2}$;
②∵$\frac{AB}{AD}=\frac{3}{2}$,
∴$\frac{BD}{AD}$=$\frac{5}{2}$,
即$\frac{10}{AD}=\frac{5}{2}$,
解得:AD=4;
故答案为:4;
③∵$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$=$\frac{3}{2}$,
∴△ABC∽△ADE,
∴$\frac{△ABC的周长}{△ADE的周长}$=$\frac{3}{2}$,
即$\frac{△ABC的周长}{16}$=$\frac{3}{2}$,
解得:△ABC的周长=24cm;
故答案为:24cm.
点评 本题考查了相似三角形的判定与性质、比例的性质;熟练掌握比例的性质,证明三角形相似是解决问题③的关键.

练习册系列答案
相关题目
15.若$\frac{m}{x-4}$-$\frac{1-x}{4-x}$=0有增根,则m的值是( )
| A. | 3 | B. | 2 | C. | -3 | D. | -2 |
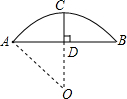 我市花园蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=8m,半径OA=5m,高度CD为2m.
我市花园蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=8m,半径OA=5m,高度CD为2m. 如图,在直角△ABC中,已知∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且∠ADC=30°,BD=18cm,则AC的长是9cm.
如图,在直角△ABC中,已知∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且∠ADC=30°,BD=18cm,则AC的长是9cm.