题目内容
14.若$\frac{1}{x(x+1)}$=$\frac{A}{x}$+$\frac{B}{x+1}$,则A=1,B=-1.分析 根据等式的性质,可得同分母分式的加减,根据同分母相等的分式的分子相等,可得关于A、B的等式,根据相等的整式的相同项的系数相等,可得答案.
解答 解:$\frac{1}{x(x+1)}$=$\frac{A}{x}$+$\frac{B}{x+1}$=$\frac{Ax+A+Bx}{x(x+1)}$,
由同分母相等的分式的分子相等,得
(A+B)x+A=1.
由相等的整式的相同项的系数相等,得
$\left\{\begin{array}{l}{A+B=0}\\{A=1}\end{array}\right.$.解得$\left\{\begin{array}{l}{A=1}\\{B=-1}\end{array}\right.$,
故答案为:1,-1.
点评 本题考查了分式的加减,利用了同分母相等的分式的分子相等,利用了相等的整式的相同项的系数相等.

练习册系列答案
相关题目
4.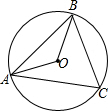 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )| A. | 50$\sqrt{3}$ | B. | $\frac{100}{3}$$\sqrt{3}$ | C. | $\frac{200}{3}$$\sqrt{3}$ | D. | 200$\sqrt{3}$ |
5.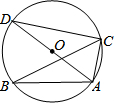 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
19.2014年天猫“双十一”整体交易额突破570亿元,570亿元用科学记数法表示为( )
| A. | 5.7×1010 | B. | 0.57×1011 | C. | 5.7×1011 | D. | 0.57×1012 |