题目内容
4.如图,直线l:$y=\frac{4}{3}x+4$交x轴于点B,交y轴于点A,⊙P过A、O两点.(1)如图①,当点P在线段OA上时,⊙P交AB于点C,求弦AC的长;
(2)如图②,当⊙P与直线l相切于点A时,求圆心点P的坐标;
(3)如图③,当点P在△AOB的外角∠OAE的平分线上时,求⊙P的半径长.
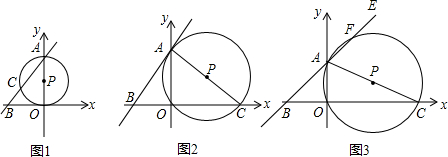
分析 (1)连接OC,先求出A、B的坐标,再根据勾股定理求出AB,然后由射影定理即可求出AC;
(2)作PD⊥x轴于D,先由切线求出∠BAC=90°,再由射影定理求出OC,得出DO、PD的长,即可得出结果;
(3)连接CF,由圆周角定理求出∠AFC=90°,根据角平分线的性质得出CF=OC,再证明△BCF∽△BAO,求出CF得出OC,最后根据勾股定理求出AC,即可得出⊙P的半径长.
解答 解:(1)连接OC,如图1所示: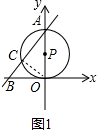 对于直线$y=\frac{4}{3}x+4$,
对于直线$y=\frac{4}{3}x+4$,
当y=0时,$\frac{4}{3}$x+4=0,解得:x=-3,
∴OB=3,B(-3,0);
当x=0时,y=4,
∴OA=4,A(0,4),
∵∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵OA是⊙P的直径,
∴∠ACO=90°,
根据射影定理得:OA2=AC•AB,
∴AC=$\frac{O{A}^{2}}{AB}$=$\frac{{4}^{2}}{5}$=$\frac{16}{5}$;
(2)作PD⊥x轴于D,如图2所示: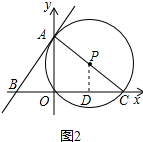
则PD∥OA,
∵⊙P与直线l相切于点A,
∴AC⊥AB,
∴∠BAC=90°,
∵OA⊥BC,
根据射影定理得:OA2=OB•OC,
∴OC=$\frac{O{A}^{2}}{OB}$=$\frac{{4}^{2}}{3}$=$\frac{16}{3}$,
∵P为AC的中点,
∴D为OC的中点,
∴DO=$\frac{1}{2}$OC=$\frac{8}{3}$,PD=$\frac{1}{2}$OA=2,
∴圆心点P的坐标为($\frac{8}{3}$,2);
(3)连接CF,如图3所示:
∵AC是直径,
∴∠AFC=90°,
∴∠AFC=∠AOB=90°,
∵AC平分∠OAE,
∴CF=OC,
又∵∠CBF=∠ABO,
∴△BCF∽△BAO,
∴$\frac{CF}{OA}=\frac{BC}{AB}$,即$\frac{CF}{4}=\frac{CF+3}{5}$,
解得:CF=12,
∴OC=12,
在Rt△AOC中,根据勾股定理得:
AC=$\sqrt{{4}^{2}+1{2}^{2}}$=4$\sqrt{10}$,
∴PA=2$\sqrt{10}$;
即⊙P的半径长为2$\sqrt{10}$.
点评 本题是圆的综合题,考查了勾股定理、圆周角定理、射影定理、角的平分线性质以及相似三角形的判定与性质;本题难度较大,综合强,特别是(3)中,根据三角形相似得出比例式求出CF,再根据勾股定理才能求出答案.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | x>$\frac{5}{4}$ | B. | x<$\frac{4}{5}$ | C. | x≥-$\frac{4}{5}$ | D. | x≤-$\frac{4}{5}$ |
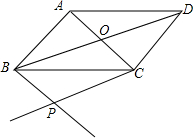 如图,?ABCD的对角线AC,BD相交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P,试判断四边形BPCO的形状,并说明理由.
如图,?ABCD的对角线AC,BD相交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P,试判断四边形BPCO的形状,并说明理由.
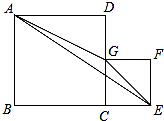 如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$.
如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$.