题目内容

5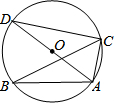．如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=35°，则∠CAD的度数是（　　）
A．35°B．45°C．55°D．65°

分析 根据圆周角定理，得∠ADC=∠ABC=35°，再根据AD是⊙O的直径，则∠ACD=90°，由三角形的内角和定理即可求得∠CAD的度数．

解答 解：∵∠ABC=35°，
∴∠ADC=35°，
∵AD是⊙O的直径，
∴∠ACD=90°，
∴∠CAD=90°-35°=55°．
故选C．

点评 本题考查了圆周角定理，直径所对的圆周角等于90°，以及三角形的内角和定理．解题的关键是：根据圆周角定理，求得∠ADC=∠ABC=35°．

练习册系列答案
相关题目
15．如图，△ABC与△A1B1C1关于直线l对称，且∠A=92°，∠C1=32°，则∠B的度数为56°．
16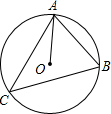．如图所示，⊙O是△ABC的外接圆，已知∠B=70°，则∠CAO的度数是（　　）
A．20°B．30°C．35°D．40°
13．下列四个实数中，是无理数的为（　　）
A．0B．$\sqrt{3}$C．-1D．$\frac{1}{3}$
20．先化简，再求值：（$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-2ab+{b}^{2}}$+$\frac{a}{b-a}$）÷$\frac{{b}^{2}}{{a}^{2}-ab}$，其中a=-1，b=$\sqrt{2}$．
10．-4的倒数是（　　）
A．4B．-$\frac{1}{4}$C．$\frac{1}{4}$D．16
17．如图，已知a∥b，小聪把三角板的直角顶点放在直线b上，若∠1=38°，则∠2的度数52°．
14．若$\frac{1}{x（x+1）}$=$\frac{A}{x}$+$\frac{B}{x+1}$，则A=1，B=-1．
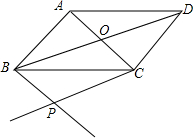15．如图，?ABCD的对角线AC，BD相交于点O，过点B作BP∥AC，过点C作CP∥BD，BP与CP相交于点P，试判断四边形BPCO的形状，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网