题目内容
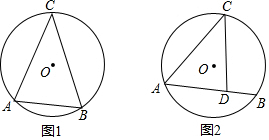
7．
如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM=x，则x的最大值是（ ）| A． | 3 | B． | $\sqrt{5}$ | C． | 2.5 | D． | 2$\sqrt{3}$ |
分析 当CD∥AB时，PM长最大，连接OM，OC，得出矩形CPOM，推出PM=OC，求出OC长即可．
解答 
解：如图：
当CD∥AB时，PM长最大，连接OM，OC，
∵CD∥AB，CP⊥CD，
∴CP⊥AB，
∵M为CD中点，OM过O，
∴OM⊥CD，
∴∠OMC=∠PCD=∠CPO=90°，
∴四边形CPOM是矩形，
∴PM=OC，
∵⊙O直径AB=5，
∴半径OC=$\frac{5}{2}$，即PM=$\frac{5}{2}$．
故选C．
点评 本题考查是圆的综合题，涉及到矩形的判定和性质，垂径定理，平行线的性质的应用，关键是找出符合条件的CD的位置，题目比较好，但是有一定的难度．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
9．下列各式计算正确的是（ ）
| A． | $\sqrt{9}$=±3 | B． | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C． | （$\sqrt{2}$）2=4 | D． | $\sqrt{27}$÷$\sqrt{3}$=3 |
如图，在平面直角坐标系中，⊙P的半径为4，圆心P坐标是（4，a）（a＞4），函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$，则a的值是4+2$\sqrt{2}$．
小明在学习13.2画轴对称图形这一节时，利用直尺和圆规完成了画一个点关于直线的对称点，其步骤如下：
