��Ŀ����
17���Ķ����ϣ�����x2-x-2=0�У�ֻ����һ��δ֪����δ֪���Ĵ���Ϊ2���������ķ��̽���һԪ���η��̣��ѷ��̵���߷ֽ���ʽ�õ���x-2����x+1��=0������֪��������ʽ�˻�Ϊ0��������һ����ʽΪ0���ɣ���˷��̿���ת��Ϊ��x-2=0��x+1=0��
��������һ�η��̵ã�x=2��x=-1��
����ԭ���̵Ľ�Ϊ��x=2��x=-1��
����������x2-x-2=0ת��Ϊx-2=0��x+1�Ĺ��̣��ǽ����ν�Ϊһ�εġ����Ρ����̣��Ӷ�ʹ������õ������
�������潵�εķ���������������⣺
��1���ⷽ��x2-3x=0��
��2��2a2-a-3=0��
��3���ⷽ���飺$\left\{\begin{array}{l}{{x}^{2}-9{y}^{2}=0}\\{x+y=4}\end{array}\right.$��
���� ��1��������߷ֽ���ʽ������������˻�Ϊ0����ʽ��������һ��Ϊ0ת��Ϊ����һԪһ�η�������⣻
��2��������߷ֽ���ʽ������������˻�Ϊ0����ʽ��������һ��Ϊ0ת��Ϊ����һԪһ�η�������⣻
��3���������һ��������߷ֽ���ʽ������������˻�Ϊ0����ʽ��������һ��Ϊ0ת��Ϊ����һԪһ�η��̣��ֱ�������⼴�ɣ�
��� �⣺��1�����̱��εã�x��x-3��=0��
�ɵ�x=0��x-3=0��
��ã�x=0��x=3��
��2�����̱��εã���2a-3����a+1��=0��
�ɵ�2a-3=0��a+1=0��
��ã�a=1.5��a=-1��
��3���������һ�����̱��εã���x+3y����x-3y��=0��
�ɵ�x+3y=0��x-3y=0��
�����ã�$\left\{\begin{array}{l}{x+3y=0}\\{x+y=4}\end{array}\right.$��$\left\{\begin{array}{l}{x-3y=0}\\{x+y=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=6}\\{y=-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$��
���� ���⿼������ʽ�ֽ��Ӧ�ã�Ū�����нⷽ�̵ķ����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
�����Ŀ
8���������x��y�ķ�����$\left\{\begin{array}{l}{4x-3y=6}\\{6x+my=26}\end{array}\right.$�Ľ�����������ô����m��ֵΪ��������
| A�� | 4��-4��-5��13 | B�� | 4��-4��-5��-13 | C�� | 4��-4��5��13 | D�� | -4��5��-5��13 |
5�� ��ͼ����ֱ������ϵ�У�ֱ��y=-x+b�뺯��y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��B����֪��A������Ϊ��3��4�������AOB���ܳ�Ϊ��������
��ͼ����ֱ������ϵ�У�ֱ��y=-x+b�뺯��y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��B����֪��A������Ϊ��3��4�������AOB���ܳ�Ϊ��������
 ��ͼ����ֱ������ϵ�У�ֱ��y=-x+b�뺯��y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��B����֪��A������Ϊ��3��4�������AOB���ܳ�Ϊ��������
��ͼ����ֱ������ϵ�У�ֱ��y=-x+b�뺯��y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��B����֪��A������Ϊ��3��4�������AOB���ܳ�Ϊ��������| A�� | 10 | B�� | 20 | C�� | 10+2$\sqrt{2}$ | D�� | 10+$\sqrt{2}$ |
12��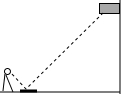 ��ͼ��С���ڵ����Ϸ���һ��ƽ�澵��ѡ����ʵ�λ�ã��պ���ƽ�澵�п�����˵Ķ�������ʱС����ƽ�澵��ˮƽ����Ϊ2m����˵ײ���ƽ�澵��ˮƽ����Ϊ16m����С�����۾���������Ϊ1.5m������˵ĸ߶�Ϊ����λ��m����������
��ͼ��С���ڵ����Ϸ���һ��ƽ�澵��ѡ����ʵ�λ�ã��պ���ƽ�澵�п�����˵Ķ�������ʱС����ƽ�澵��ˮƽ����Ϊ2m����˵ײ���ƽ�澵��ˮƽ����Ϊ16m����С�����۾���������Ϊ1.5m������˵ĸ߶�Ϊ����λ��m����������
 ��ͼ��С���ڵ����Ϸ���һ��ƽ�澵��ѡ����ʵ�λ�ã��պ���ƽ�澵�п�����˵Ķ�������ʱС����ƽ�澵��ˮƽ����Ϊ2m����˵ײ���ƽ�澵��ˮƽ����Ϊ16m����С�����۾���������Ϊ1.5m������˵ĸ߶�Ϊ����λ��m����������
��ͼ��С���ڵ����Ϸ���һ��ƽ�澵��ѡ����ʵ�λ�ã��պ���ƽ�澵�п�����˵Ķ�������ʱС����ƽ�澵��ˮƽ����Ϊ2m����˵ײ���ƽ�澵��ˮƽ����Ϊ16m����С�����۾���������Ϊ1.5m������˵ĸ߶�Ϊ����λ��m����������| A�� | $\frac{16}{3}$ | B�� | 9 | C�� | 12 | D�� | $\frac{64}{3}$ |
2��������mx+ny=6����������$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$����mn��ֵΪ��������
| A�� | 8 | B�� | -8 | C�� | 9 | D�� | -9 |
9����֪�����������߷ֱ���1��$\sqrt{3}$��2�����������Ϊ��������
| A�� | ��������� | B�� | ֱ�������� | C�� | �۽������� | D�� | ��ȷ�� |
6������a2•a3�Ľ�����ڣ�������
| A�� | a5 | B�� | a9 | C�� | a6 | D�� | a-1 |