题目内容
1.一个直角三角形的两直角边长分别为5和12,则它斜边上的高长为( )| A. | 13 | B. | $\frac{13}{2}$ | C. | $\frac{60}{13}$ | D. | $\frac{12}{5}$ |
分析 先用勾股定理求出斜边长,然后再根据直角三角形面积的两种公式求解即可.
解答 解:∵直角三角形的两直角边长分别为5和12,
∴斜边长=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴斜边的高=$\frac{5×12}{13}$=$\frac{60}{13}$.
故选C.
点评 本题考查勾股定理及直角三角形面积,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
12.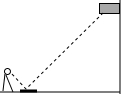 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )| A. | $\frac{16}{3}$ | B. | 9 | C. | 12 | D. | $\frac{64}{3}$ |
9.已知三角形三条边分别是1、$\sqrt{3}$、2,则该三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
6.计算a2•a3的结果等于( )
| A. | a5 | B. | a9 | C. | a6 | D. | a-1 |
13.把一根长17m的钢管截成2m和3m长两种规格的钢管,在不造成浪费的情况下你的截法有( )
| A. | 5种 | B. | 4种 | C. | 3种 | D. | 2种 |
 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,若△OPnPn+1的面积大于6时,n至少是144.
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,若△OPnPn+1的面积大于6时,n至少是144.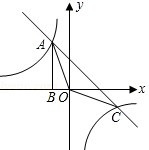 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$. 如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.
如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.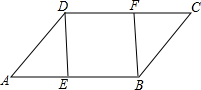 如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF.
如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF.