题目内容
4.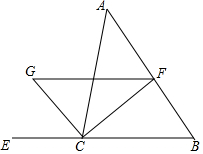 如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
分析 首先利用三角形的外角等于不相邻的两个内角的和求得∠ACE的度数,然后根据角的平分线的定义求得∠GCE的度数,再利用平行线的性质求得∠FGC;利用角的平分线的定义可以得到∠FCG=∠ACF+∠ACG=$\frac{1}{2}$(∠ACB+∠ACE),从而求得∠FCG.
解答 解:∵∠ACE=∠A+∠B=45°+55°=100°,
又∵CG是∠ACE的平分线,
∴∠GCE=∠ACG=$\frac{1}{2}$∠ACE=50°,
∵FG∥BC,
∴∠FGC=∠GCE=50°.
∵CF平分∠ACB,
∴∠ACF=$\frac{1}{2}$∠ACB,
又∵∠ACG=$\frac{1}{2}$∠ACE,
∴∠FCG=∠ACF+∠ACG=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠ACE=$\frac{1}{2}$×180°=90°.
点评 本题考查了三角形角的平分线以及三角形的外角的性质,证得∠FCG=$\frac{1}{2}$(∠ACB+∠ACE)是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.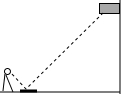 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )| A. | $\frac{16}{3}$ | B. | 9 | C. | 12 | D. | $\frac{64}{3}$ |
19.如图1,在平面直角坐标系中,将?ABCD放置在第一象限,且AB∥x 轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,则□ABCD的面积为( )
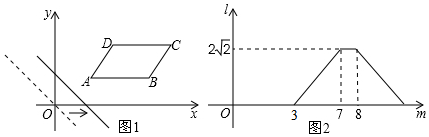

| A. | 10 | B. | 10$\sqrt{5}$ | C. | 5 | D. | 5$\sqrt{5}$ |
9.已知三角形三条边分别是1、$\sqrt{3}$、2,则该三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
13.把一根长17m的钢管截成2m和3m长两种规格的钢管,在不造成浪费的情况下你的截法有( )
| A. | 5种 | B. | 4种 | C. | 3种 | D. | 2种 |
14.一个角的余角是它的2倍,这个角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
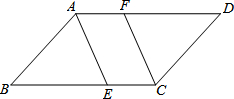 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:DF=BE.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:DF=BE.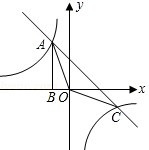 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$.