题目内容
20.如果-$\frac{2}{3}\sqrt{6-3x}$是二次根式,那么x应满足的条件是( )| A. | x≥0 | B. | x≥2 | C. | x≤2 | D. | x<6 |
分析 根据二次根式有意义的条件可知6-3x≥0,解出x的范围即可.
解答 解:由题意可知:6-3x≥0,
∴x≤2
故选(C)
点评 本题考查二次根式的定义,解题的关键是正确理解二次根式有意义的条件,本题属于基础题型.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8.如果关于x,y的方程组$\left\{\begin{array}{l}{4x-3y=6}\\{6x+my=26}\end{array}\right.$的解是整数,那么整数m的值为( )
| A. | 4,-4,-5,13 | B. | 4,-4,-5,-13 | C. | 4,-4,5,13 | D. | -4,5,-5,13 |
5. 如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
 如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )| A. | 10 | B. | 20 | C. | 10+2$\sqrt{2}$ | D. | 10+$\sqrt{2}$ |
12.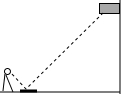 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )| A. | $\frac{16}{3}$ | B. | 9 | C. | 12 | D. | $\frac{64}{3}$ |
9.已知三角形三条边分别是1、$\sqrt{3}$、2,则该三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a)
运动时心跳速率通常和人的年龄有关,用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每份周心跳的最高次数,则b=0.8(220-a) 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,若△OPnPn+1的面积大于6时,n至少是144.
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,若△OPnPn+1的面积大于6时,n至少是144.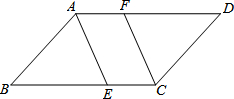 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:DF=BE.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:DF=BE. 如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.
如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.