题目内容
4.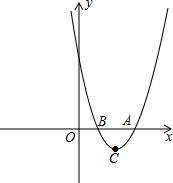 如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.
如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.(1)求点A、C的坐标;
(2)求抛物线y=x2-4x+3关于y轴对称的抛物线的表达式;
(3)设(2)中所求抛物线上的点A1与点A对应,顶点C1与点C对应,在抛物线y=x2-4x+3上是否存在一点P,使△PA1C1的面积最小?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)列方程即可得A(3,0),根据二次函数的顶点坐标公式即可得到C(2,-1);
(2)根据关于y轴对称的图象的特点即可得到结论;
(3)根据已知条件得到A1(-3,0),C1(-2,-1),求得直线A1C1的解析式为y=-x-3,由于△PA1C1的面积最小,得到P到A1C1的距离最小,设P(m,m2-4m+3),P到A1C1的距离为W,根据点到直线的距离公式即可得到结论.
解答 解:(1)∵抛物线y=x2-4x+3的顶点为C,与x轴交于A,
∴令y=0,即x2-4x+3=0,
∴x1=1,x2=3,
∴A(3,0),
∴-$\frac{b}{2a}$=2,$\frac{4ac-{b}^{2}}{4a}$=-1,
∴C(2,-1);
(2)抛物线y=x2-4x+3关于y轴对称的抛物线的表达式为y2=x2+4x+3;
(3)∵抛物线y=x2-4x+3与抛物线y1=x2+4x+3关于y轴对称,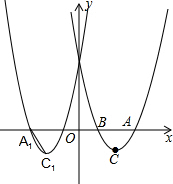
∵A(3,0),C(2,-1),
∴A1(-3,0),C1(-2,-1),
∴直线A1C1的解析式为y=-x-3,
∵△PA1C1的面积最小,
∴P到A1C1的距离最小,
设P(m,m2-4m+3),P到A1C1的距离为W,
则W=$\frac{|m+{m}^{2}-4m+3+3|}{\sqrt{{1}^{2}+{1}^{2}}}$=$\frac{|{m}^{2}-3m+6|}{\sqrt{2}}$,
要使W的值最小,则|x2-3x+6|最小,
即x2-3x+6=0,
∵x2-3x+6=0无实根,
∴不存在点P,使△PA1C1的面积最小.
点评 本题主要考查待定系数法求函数解析式和函数与x轴的交点坐标,点到直线的距离公式,在(3)中知道当△PA1C1的面积最小时,P到A1C1的距离最小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一次函数y=4x+1,当x>0时,y的取值范围为( )
| A. | y>0 | B. | y<0 | C. | y>1 | D. | 0<y<1 |
19.下表记录了小敏等四名学生五次数学测验成绩的平均数与方差:
根据表中数据,要从中挑选一名成绩好又比较稳定的同学参加我区的数学头脑运动会,你认为应该选( )
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
9.某班派9名同学参加红五月歌咏比赛,他们的身高分别是(单位:厘米):167,159,161,159,163,157,170,159,165.这组数据的众数和中位数分别是( )
| A. | 159,163 | B. | 157,161 | C. | 159,159 | D. | 159,161 |
16.已知关于x的不等式组$\left\{\begin{array}{l}x-a>0\\ 7-2x>1\end{array}\right.$有且只有1个整数解,则a的取值范围是( )
| A. | a>1 | B. | 1≤a<2 | C. | 1<a≤2 | D. | a≤2 |
13.若关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=-4,则m+n的值是( )
| A. | -10 | B. | 10 | C. | -6 | D. | -1 |
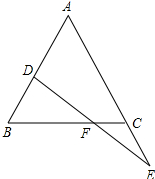 已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.
已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.