题目内容
10. 已知点A(2,-2)和点B(-4,n)在抛物线y=ax2(a≠0)上.
已知点A(2,-2)和点B(-4,n)在抛物线y=ax2(a≠0)上.(1)求a的值及点B的坐标;
(2)点P在y轴上,且△ABP是以AB为直角边的三角形,求点P的坐标;
(3)将抛物线y=ax2(a≠0)向右并向下平移,记平移后点A的对应点为A′,点B的对应点为B′,若四边形ABB′A′为正方形,求此时抛物线的表达式.
分析 (1)把点A(2,-2)代入y=ax2,得到a,再把点B代入抛物线解析式即可解决问题.
(2)求出直线AB解析式,再分别求出过点A垂直于AB的直线的解析式,过点B垂直于直线AB的解析式即可解决问题.
(3)先求出点A′坐标,确定是如何平移的,再确定抛物线顶点的坐标即可解决问题.
解答 解:(1)把点A(2,-2)代入y=ax2,得到a=-$\frac{1}{2}$,
∴抛物线为y=-$\frac{1}{2}$x2,
∴x=-4时,y=-8,
∴点B坐标(-4,-8),
∴a=-$\frac{1}{2}$,点B坐标(-4,-8).
(2)设直线AB为y=kx+b,则有$\left\{\begin{array}{l}{-4k+b=-8}\\{2k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$,
∴直线AB为y=x-4,
∴过点B垂直AB的直线为y=-x-12,与y轴交于点P(0,-12),
过点A垂直AB的直线为y=-x,与y轴交于点P′(0,0),
∴点P在y轴上,且△ABP是以AB为直角边的三角形时.点P坐标为(0,0),或(0,-12).
(3)如图四边形ABB′A′是正方形,过点A作y轴的垂线,过点B、点A′作x轴的垂线得到点E、F.
∵直线AB解析式为y=-x-12,∴△ABF,△AA′E都是等腰直角三角形,
∵AB=AA′=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
∴AE=A′E=6,
∴点A′坐标为(8,-8),
∴点A到点A′是向右平移6个单位,向下平移6个单位得到,
∴抛物线y=-$\frac{1}{2}$x2的顶点(0,0),向右平移6个单位,向下平移6个单位得到(6,-6),
∴此时抛物线为y=-$\frac{1}{2}$(x-6)2-6.
点评 本题考查二次函数图象上点的特征、一次函数等知识,解题的关键是学会待定系数法确定函数解析式,知道两条直线垂直k的乘积为-1,属于中考常考题型.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案 如图,在平行四边形ABCD中,BE平分∠ABC,BC=6,DE=1,则平行四边形ABCD的周长等于22.
如图,在平行四边形ABCD中,BE平分∠ABC,BC=6,DE=1,则平行四边形ABCD的周长等于22.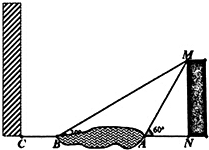 根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.
根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上. 如图,直线a∥b,∠1=110°,∠2=60°,则∠3的度数为50°.
如图,直线a∥b,∠1=110°,∠2=60°,则∠3的度数为50°.