题目内容
12.已知:-$\sqrt{3}$是a的一个平方根,b是平方根等于本身的数,c是$\sqrt{32}$的整数部分,求$\sqrt{2a+b+2c}$的平方根.分析 先根据平方根和$\sqrt{32}$的范围求出a、b、c的值,代入求出$\sqrt{2a+b+2c}$的值,再求出平方根即可.
解答 解:∵-$\sqrt{3}$是a的一个平方根,b是平方根等于本身的数,c是$\sqrt{32}$的整数部分,
∴a=3,b=0,c=5,
∵$\sqrt{2a+b+2c}$=$\sqrt{16}$=4,
∴$\sqrt{2a+b+2c}$的平方根是±2.
点评 本题考查了估算无理数的大小,平方根等知识点,能求出a、b、c的值是解此题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.若代数式$\frac{\sqrt{3x-2}}{|x|-3}$有意义,则x的取值范围是( )
| A. | x>$\frac{2}{3}$且x≠3 | B. | x≥$\frac{2}{3}$ | C. | x≥$\frac{2}{3}$且x≠3 | D. | x≤$\frac{2}{3}$且x≠-3 |
 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点). 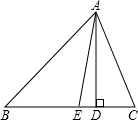 如图,在△ABC中,AD是边BC上的高,AE平分∠BAC,∠B=40°,∠C=68°,求∠AEC和∠DAE的度数.
如图,在△ABC中,AD是边BC上的高,AE平分∠BAC,∠B=40°,∠C=68°,求∠AEC和∠DAE的度数.