题目内容
9.关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{3-2x>-1}\end{array}\right.$的整数解共有5个,则a的取值范围( )| A. | a=-3 | B. | -4<a<-3 | C. | -4≤a<-3 | D. | -4<a≤-3 |
分析 首先解不等式组确定不等式组的解集,然后根据不等式的整数解有5个,即可得到一个关于a的不等式组,解不等式组即可求解.
解答 解:$\left\{\begin{array}{l}{x-a≥0①}\\{3-2x>-1②}\end{array}\right.$,
解①得:x≥a,
解②得:x<2,
则不等式组的解集是:a≤x<2,
不等式组有5个整数解,则-4<a≤-3,
故选D.
点评 此题考查的是一元一次不等式的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
4.下列命题是真命题的是( )
| A. | 同位角相等 | |
| B. | 有且只有一条直线与已知直线垂直 | |
| C. | 垂线段最短 | |
| D. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 |
14.下列计算,正确的是( )
| A. | a2-a=a | B. | a2•a3=a6 | C. | a9÷a3=a3 | D. | (a3)2=a6 |
18.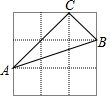 如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
 如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
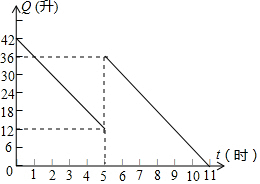 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.